Ruch w polu grawitacyjnym: Prawa Keplera

Zagadnienie dwóch ciał poruszających się pod wpływem wzajemnego przyciągania grawitacyjnego można łatwo sprowadzić do zagadnienia ruchu względnego (patrz Dodatek). Zamiast dwóch wektorów położenia  r1 i r2  posługujemy się wektorem położenia względnego .

Równanie ruchu przyjmuje postać

 

                                                                                      (1)

gdzie μ oznacza masę zredukowaną:

                                                                                            (2)

Zagadnienie sprowadzone zostało formalnie do ruchu jednego ciała o masie μ. Warto zauważyć, że w przypadku gdy jedna z mas jest znacznie mniejsza od drugiej (np. ruch planety wokół Słońca), masa zredukowana jest praktycznie równa tej mniejszej masie.

 

Zachowanie momentu pędu: II prawo Keplera

Łatwo sprawdzić, że w zagadnieniu jednego ciała zachowany jest moment pędu

 

                                                                                                    (3)

Różniczkując otrzymujemy bowiem (dalej zamiast oznaczeń M1, M2 używamy M,m)

 

                                                           

 

Wektor J jest zatem stały co do wartości i kierunku. Oznacza to, że ruch jest płaski i zachodzi w płaszczyźnie prostopadłej do J. Położenie cząstki na tej płaszczyźnie opisać możemy za pomocą współrzędnych biegunowych  Wprowadzając wersory

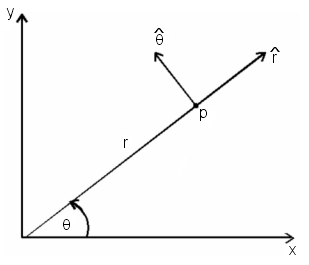
rys. 1

 jak na rys. 1, prędkość przedstawić możemy następująco

 

                                                                                 

ponieważ  jest prędkością kątową. Moment pędu równy jest

 

                                                                  (4)

                                                                                                                                             

gdzie  oznacza wektor jednostkowy  prostopadły do płaszczyzny ruchu.

Łatwo sprawdzić, że moment pędu jest proporcjonalny do szybkości zakreślania pola przez wektor wodzący  Pole ∆S zakreślane w czasie ∆t równe jest bowiem, jak widać z rysunku 2,

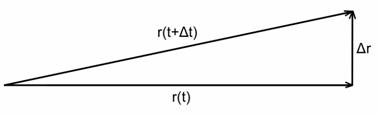
Rys. 2

.                                                                                                

Mamy więc

 

                                                                                                 

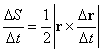
i w granicy ∆t®0

 

.                                                                                                   

 

Moment pędu (3) równy jest zatem co do wartości

 

.                                                                                                  (4’)

 

Zachowanie momentu pędu oznacza, że szybkość zakreślania pola jest stała. Inaczej mówiąc, w jednakowych odstępach czasu wektor  zakreśla jednakowe pola. Wniosek ten nazywa się II prawem Keplera. Rys. 3 przedstawia II prawo Keplera w przypadku orbity eliptycznej.

 

 

 

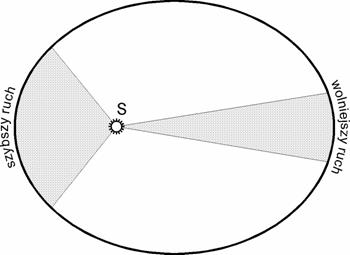
Rys. 4. Zaznaczone pola są jednakowe i odpowiadają jednakowym czasom.

 

Kształt toru: I prawo Keplera

Jeśli , to istnieje punkt, w którym odległość ciała od centrum siły jest minimalna. Możemy wybrać oś Ox tak, aby pokrywała się z kierunkiem perihelium ciała (por. rys. 5).

 

 

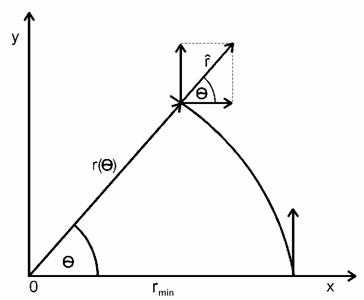
Rys. 5

 

Równanie ruchu  (1)  możemy przekształcić korzystając z definicji prędkości:

                                                                                                             

do postaci:

                                                                                             

Lewą stronę ostatniego równania można zapisać

 

                                                                                       

Jeśli skorzystać z wyrażenia (4) na moment pędu:

 

                                                                                                     

i podstawić  do równania ruchu, dostaniemy

 

                                                                                    

a po uproszczeniu

 

                                                                                            (5)

Dalej, jak widać z rysunku 5

 

.                                                                                              

Równanie (5) oznacza więc, że

 

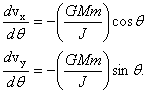                                                                             (5’)

 

Wyrażenie w nawiasie jest stałe, więc całkowanie tego układu jest trywialne:

 

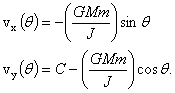                                                                           (6)

 

C jest stałą całkowania oraz uwzględniamy, że zgodnie z rysunkiem 5 vx(0) = 0.

 

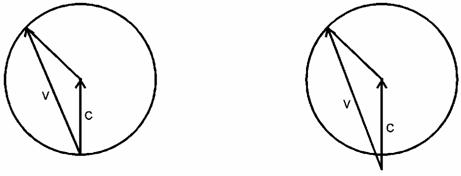
Równania (6) i możliwe przypadki ruchu ciała można przedstawić graficznie. Jeśli wektor [O, C] oznaczymy przez C, to łatwo sprawdzić, że długość wektora  jest stała i równa . Oznacza to, że koniec wektora v leży zawsze na okręgu. Możliwe sytuacje przedstawia rys. 6.

 

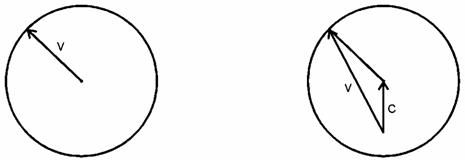
                                              C = 0                                                                                    

 

                                                                                                                   

Rys. 6

 

 

 

Obliczając teraz momentu pędu, równy swej z – owej składowej Jz, mamy

 

                                           

Po podstawieniu związków (6) otrzymujemy

 

                                                                                

Obliczając stąd  r mamy

 

                                                                                       

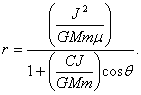
Jest to znane z geometrii analitycznej równanie biegunowe stożkowej, centrum sił znajduje się w jej ognisku,

 

                                                                                                 

gdzie e oznacza mimośród, a p parametr. Zatem torem ciała jest jedna z krzywych stożkowych: elipsa, parabola bądź hiperbola. Jest to treść I prawa Keplera.

 

Porównując dwa ostatnie równania otrzymujemy parametr i mimośród stożkowej w postaci:

                                                                                                                                             (7a)

                                                                                                                                (7b)

 

Łatwo zauważyć, że cztery sytuacje przedstawione na rysunku 6 odpowiadają zgodnie z równaniem (7b) różnym wartościom mimośrodu orbity e. Mamy kolejno: okrąg (e=0), elipsę (e<1), parabolę (e=1) oraz hiperbolę (e>1).

III prawo Keplera

Z powyższych rozważań możemy też wyprowadzić III prawo Keplera. W tym przypadku zakładamy, że orbita jest elipsą. Z równania (4’) mamy:

 

.                                                                                                         

Z kolei z prawa pól wynika, że

 

.                                                                                                       

 

Porównując oba równania i podnosząc do kwadratu otrzymujemy

 

.                                                                                            (8)

Ponieważ

                   b2 = a2(1-e2) = ap                                                                                              

równanie (8) przyjmuje postać

 

.                                                                                                

Podstawiając do ostatniego równania wyrażenie (7a) na  parametr p:

 

,                                                                                                   

otrzymujemy

 

,

czyli

.                                                                                          

Jest to III prawo Keplera.

 

Dodatek: Zagadnienie dwóch ciał i ruch względny

Rys. 7

 

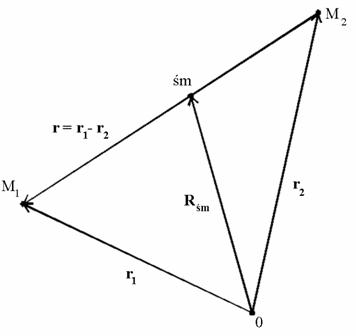
Dla dwóch jednorodnych ciał kulistych działających na siebie siłami grawitacji równania ruchu mają postać:

                                             

gdzie  

Po dodaniu obu równań stronami otrzymujemy

 

                                                                                             

Powtyższe równanie przedstawia zasadę zachowania pędu całego układu, ponieważ po jego obustronnym zcałkowaniu otrzymamy

 

                                                                                  (9)

gdzie lewa strona przedstawia całkowity pęd układu.

Położenie środka masy określa wzór

 

                                                                                        

Różniczkując jego obie strony względem czasu otrzymamy

 

                                                                                        

Z równania (9) otrzymujemy, że  co oznacza, że środek masy porusza się ze stałą prędkością. Można zawsze dobrać inercjalny układ odniesienia, w którym ta prędkość jest równa zeru.

Jeśli równania ruchu przekształcimy do postaci

 

                                             

i odejmiemy stronami otrzymamy

 

                                                

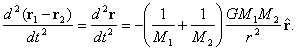
To równanie zawiera tylko jeden wektor .

Po wprowadzeniu masy zredukowanej μ zdefiniowanej wzorem:

 

                                                                                                

ostatenie równanie przyjmie postać

 

                                                                                         

W ten sposób zagadnienie dwóch ciał wymagające wyznaczenia dwóch wektorów ,  zostało sprowadzone do zagadnienia jednego ciała, w którym należy wyznaczyć zależność jednego wektora r od czasu. Ruch ciała  określamy względem .