ŚWIATŁO I ROZUM

Bóg wynalazł wzrok i obdarzył nas nim, abyśmy oglądając na niebie periodyczne ruchy ro­zu­mu wykorzystywali je w obrotach naszego rozumu, które są spokrewnione z tamtymi ruchami, chociaż są one uporządkowane, a te w nas bywają niekiedy zakłócane […]

Platon, Timajos

W XVII wieku zobaczono tyle nowego na niebie i na ziemi, że nie sposób było uniknąć pytań, czym właściwie jest światło, skąd biorą się kolory, czy obrazy widziane w lunecie albo mikroskopie nie są tylko złudzeniami. Jeszcze na początku wieku uczeni koledzy Galileusza odmawiali spojrzenia przez teleskop, nie chcąc zaświad­czać powagą swego autorytetu, że widziany w nim obraz jest czymś więcej niż jarmarczną sztuczką. Teorie objaśniające, jak tworzy się obraz w lunecie, powstały dopiero później. Niełatwo dziś ustalić, czy coraz powszechniejsze zaufanie do przyrządów optycznych było skutkiem rozwoju nauki i doskonalenia samych przyrządów, czy raczej postępującego przyzwyczajenia.

Światło – coś, czego nie da się pochwycić, zatrzymać, dotknąć, zamknąć w butelce – sprawiało wiele kłopotu i fascynowało filo­zo­fów mechanistycznych. Objaśnienie zjawisk świetlnych było ro­dza­jem tour de force dla ich systemów, próbą, z której wszelako żaden z nich nie wyszedł bez szwanku. W dyskusjach na temat optyki widać również, jak łatwo było pokonać Arystotelesa w kate­go­riach ogólnych i jak trudno było uwolnić się od tradycji w niezli­czonych kwestiach szczegółowych. W rezultacie siedemnastowieczna opty­ka bardziej przypomina plac budowy niż skończony gmach.

Optyka starożytna była przede wszystkim teorią widzenia, a wła­ś­ci­wie wieloma sprzecznymi poglądami na jego temat. Zdaniem Arystotelesa wzrok postrzega nie światło, lecz barwę przedmiotu. Światło natomiast jest tym czymś, co sprawia, że potencjalnie przez­roczyste ciała, jak powietrze czy woda, stają się przezroczyste aktu­alnie, tzn. pozwalają dostrzec barwy – „światło jest aktem rzeczy przezroczystej jako przezroczystej” – jak to ujmował. Było to naukowe wyjaśnienie, dlaczego nie widzimy w nocy, choć powie­trze jest nadal przezroczyste: do widzenia barw potrzeba jeszcze światła.

Światło nie istnieje samodzielnie, nie jest substancją, lecz tylko „obecnością ognia lub czegoś tego rodzaju w materii przezro­czystej”. Całe zjawisko widzenia nie wiąże się u Arystotelesa z żad­nym ruchem przestrzennym. Barwy, jakie obserwujemy, powsta­ją z ułożenia obok siebie cząstek białych i czarnych, tak małych, że niedostrzegalnych okiem. Z modyfikacji czy osłabienia bieli po­wstają kolejne barwy – od jasnej czerwieni, gdy osłabienie jest nieznaczne, aż po najsłabszy fiolet, graniczący z ciemnością.

Obok filozoficznej teorii Arystotelesa istniała w optyce geomet­ryczna teoria promieni wzrokowych. Miały one tworzyć stożek z wierz­chołkiem w oku: człowiek kierując wzrok w daną stronę wysy­łałby z oka w odpowiednim kierunku wiązkę promieni. Starożytni sformułowali dla promieni wzrokowych prawo odbicia i badali również prawo załamania. Ptolemeusz podaje (bez komen­tarzy) dość dokładną tabelkę kątów padania i załamania w wodzie, która jest, jak wykazały to współczesne badania, wynikiem pomiarów dla kilku kątów i następnie dopasowania do tych danych zależności kwadratowej – choć nie miało to żadnego uzasadnienia teoretycznego.

Na początku XVII w. optyka była już dziedziną z bardzo długą tradycją od starożytności przez arabskie i łacińskie średniowiecze. Pierwszą pracą formułującą zasady optyki geometrycznej i działania wzroku w sposób, w jaki do dziś przedstawia się te zagadnienia w szkołach, była książka Keplera Ad Vitellionem paralipomena, 1604 (Para­li­pomena do Witelona). Sam tytuł nawiązujący do trzynasto­wiecznego uczonego ze Śląska Witelona świadczy o powolnym tempie przemian w świecie wiedzy i akademickiego nauczania. Pomimo tego konserwatywnego tytułu dzieło formułuje po raz pierw­szy zasadę prostoliniowego rozchodzenia się światła we wszys­tkich kierunkach z każdego punktu świecącego przedmiotu. Objaśnia też optyczną konstrukcję oka: jest ono rodzajem camera obscura, w której światło wpadające przez źrenicę tworzy obraz przedmiotu na siatkówce. Rogówka i soczewka oka potrzebne są do wytworzenia ostrego obrazu. Obraz w camera obcura jest co prawda odwrócony, ale abstrakcyjnie rozumującemu Keplerowi zu­peł­nie to nie przeszkadzało. To Kepler kilka lat później miał podać zasadę budowy teleskopu astronomicznego, w którym również obraz jest odwrócony.

Wyjaśnienie roli oka w tworzeniu się obrazów pozwoliło na rozdzielenie teorii widzenia i optyki. Oko stało się przyrządem opty­cznym o znanym działaniu. Aż do utworzenia się obrazu na siat­­kówce można posługiwać się optyką, a objaśnienie, w jaki spo­sób obraz z siatkówki może zostać przekazany do mózgu i zrozu­miany, należy już do fizjologii.

Kepler pierwszy przedstawia tworzenie się obrazów jako odw­zo­ro­wanie punktów przedmiotu na punkty obrazu. Oznacza to, że nie istnieje nigdzie w świecie zewnętrznym gotowy obraz przed­miotu, lecz tworzy się dopiero punkt po punkcie na siatkówce oka. Całość obrazu jest po prostu sumą jego części. Nie tylko nie po­strze­gamy przedmiotów bezpośrednio takimi, jakimi są, lecz nawet nie postrzegamy ich jako wyodrębnionych całości, widzimy jedynie zbiór świetlnych punktów.

Działanie soczewek i lunety było tematem następnego traktatu optycznego Keplera Dioptrice, 1611 (Dioptryka; dioptryka była jednym z tradycyjnych działów nauki o świetle, zajmującym się załamaniem), napisanego już po zastosowaniu lunety do obserwacji astronomicznych przez Galileusza. Sam Galileusz nie rozumiał zasa­dy działania swego przyrządu, nie dysponował żadną teorią mate­ma­tyczną na jego temat – co było zresztą typowe przy wpro­wadzaniu wielu wynalazków.

Kepler usiłował również odkryć matematyczne prawo zała­ma­nia. Wypróbował w tym celu wiele formuł trygonometrycznych, jednak bez powodzenia. Jedną z przyczyn było, jak się zdaje, określenie przez niego kąta załamania jako kąta odchylenia promienia od pierwotnego kierunku – przy takim określeniu wzór jest bardziej skomplikowany. W zastosowaniu do soczewek wystar­czała przybliżona wersja prawa słuszna dla niemal prostopadłego padania, lecz prawo słuszne dla wszystkich kątów sformułował dopiero Willebrord Snell. Snell nie opublikował swoich badań i prawo załamania zostało ogłoszone po raz pierwszy dopiero w 1637 r. przez Kartezjusza w jego La dioptrique (Dioptryka), która była jedną z trzech rozpraw dołączonych do Rozprawy o metodzie jako przykład zastosowania filozoficznej metody autora. Dwie po­zo­stałe to La géométrie (Geometria) i Les météores (Meteory).

W Dioptryce Kartezjusz nie zajmuje się naturą światła, przed­stawia jednak trzy porównania pozwalające wnioskować o jego właściwościach. Metodę postępowania porównuje z tym, co robią astronomowie, którzy na podstawie arbitralnych założeń otrzymują wnioski zgodne z obserwacjami. Według pierwszego porównania światło przypominałoby pewien ruch lub działanie, a widzenie byłoby podobne do macania laską przez ślepca. Laska ta wrażliwa byłaby również na pewne ruchy, które związane są z barwą. Nietrudno też byłoby pojąć, dlaczego światło rozchodzi się natych­  miastowo (jak sądził Kartezjusz). Drugie porównanie ma przy­bliżyć konsekwencje faktu, że świat jest wypełniony materią. Wyobraźmy sobie kadź pełną na wpół wytłoczonych winogron i winnego moszczu w porze winobrania. Jeśli w dnie kadzi zrobimy mały otwór, wino natychmiast zacznie wypływać. Wino z różnych punk­tów kadzi dąży prostoliniowo w stronę otworu – co ma wyjaśniać prostoliniowe rozchodzenie się światła, które jest „skłonnością do ruchu” eteru (wina), a nie samym ruchem. Ruch bowiem nie mógł­by zachodzić jednocześnie w różnych kierunkach, jak rozchodzi się światło. Ruch eteru nie mógłby też być prostoliniowy – przeszka­dza­łyby w tym cząstki grubszej materii – winogrona z porównania. „Skłonności do ruchu” w różne strony nie przeszkadzają sobie wzajemnie, podobnie jak nie przesz­kadzają sobie wzajemnie promienie świetlne biegnące w różnych kierunkach. Światło nie jest więc niczym materialnym ani nie jest też ruchem.

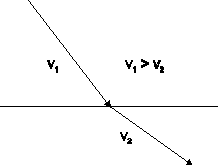Ryc. 1 Ilustracja prawa załamania według Kartezjusza

W trzecim porównaniu Kartezjusz zakłada jednak, że „skłonność do ruchu” – światło – podlega tym samym prawom co ruch i moż­na zamiast światła rozważać tor piłki tenisowej odbijającej się od powierzchni bądź wpadającej na przykład do wody. Dla piłki prawa odbicia i załamania otrzymujemy przyjmując, że składowa prędkości wzdłuż granicy ośrodków nie zmienia się. Jeśli w drugim ośrodku całkowita prędkość piłki zmaleje, to jej tor odchyli się w kierunku granicy rozdziału obu ośrodków (ryc. 1), a odpowied­nie kąty będą spełniać prawo załamania. Kartezjusz nie wyjaśnia, co w naturze miałoby być odpowiednikiem prędkości piłki z porów­nania – według niego światło rozchodzi się przecież momentalnie w obu ośrodkach. W ten sposób sformuło­wane zostało ściśle prawo załamania i pewna jego interpretacja teoretyczna. Nie wiadomo, czy Kartezjusz znał pracę Snella. Miesz­kał w Holandii i obracał się w niewielkim środowisku uczonych, w którym informacje rozchodziły się dość szybko, sam oczywiście nic nie wspomina o jakichkolwiek poprzednikach. Niezależnie jednak od tego, czy znał ją, czy nie, jego zasługą pozostanie pierwsza próba zrozumienia tego prawa, jednego z kilku znanych wtedy matematycznych praw przyrody.

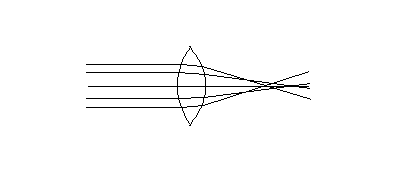Ryc. 2 Aberracja sferyczna

Kartezjusz nie wykonał żadnych pomiarów, aby upewnić się co do słuszności prawa załamania. Analogia do ruchu piłki tenisowej wydawała mu się wystarczająco ścisła. W Dioptryce zastosował prawo załamania do najważniejszego zadania praktycznego ówczes­nej optyki – zbadał możliwości ulepszenia przyrządów op­ty­cznych. Obraz w ówczesnych przyrządach optycznych był zabar­wiony i często zniekształcony do tego stopnia, że rozpoznanie praw­dzi­wego kształtu obiektu nie było wcale łatwe. Na przykład przez kilka dziesięcioleci dyskutowano nad kształtem planety Saturn, która każdemu obserwatorowi zdawała się inna. Gdy zau­wa­żo­no, że stosowanie soczewek o bardzo długiej ogniskowej pozwala zmniejszyć wpływ wad optycznych, zaczął się wyścig w budowaniu coraz dłuższych teleskopów. Składały się one z obiektywu i oku­laru, osadzonych na długim pręcie – były to tzw. télescopes aérienes – teleskopy powietrzne. Przyrządy te, stosowa­ne przez najlepszych astronomów epoki, takich jak Cassini, bracia Huygensowie czy Heweliusz, osiągały długość dwustu stóp i były wyjątkowo trudne w obsłudze. Dzięki takim właśnie teleskopom dokonano większości odkryć w astronomii planetarnej XVII w. Dalsze zwiększanie długości było wszakże niemożliwe, przyrządy stały się nie tylko niewygodne, lecz również drgania konstrukcji utrudniały obser­wacje, potrzebne były nowe idee.

Kartezjusz wykazał, że zwykła soczewka o sferycznych powierzch­niach nie skupia w jednym punkcie wszystkich pa­dających na nią promieni równoległych (ryc. 2). Jest to tzw. obecnie aberracja sferyczna. Soczewka taka nie może więc wytworzyć ostrego obrazu odległego przedmiotu. Posługując się prawem załamania i swą znajomością geometrii Kartezjusz udowodnił, że odpowiednio dobrane powierzchnie eliptyczne i hiperboliczne mogą idealnie ogniskować światło. Teoretycznie problem był rozwiązany i wyda­wa­ło się, że wystarczy opracować metodę szlifowania soczewek o kształcie przecięć stożkowych. Zadaniem tym zajęło się wielu uczo­nych i współpracujących z nimi rzemieśl­ników, rzecz okazała się jednak bardzo trudna. Szlifowanie powierzchni sferycznych od­by­wało się przez docieranie dwóch powierzchni, wklęsłej i wypuk­łej, za pomocą ruchów w różne strony, co nie jest możliwe w przypadku powierzchni innego kształtu niż sferyczna.

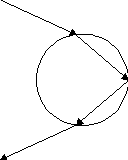Ryc. 3 Tworzenie się tęczy

Druga z rozpraw Kartezjusza, Meteory, zawiera najważniejsze pojedyncze osiągnięcie Kartezjusza w naukach przyrodniczych: objaś­nie­nie zjawiska tęczy, które było zresztą powodem napisania całej rozprawy. Tęczą zajmowało się wielu autorów od czasu Arystotelesa, lecz dopiero Kartezjuszowi udało się objaśnić, dlacze­go łuk tęczy tworzy stały kąt z kierunkiem słońca. Już wcześniej zjawisko tęczy łączono z odbiciami i załamaniem światła słonecz­nego w kropelkach wody, próbowano też badać to zjawisko ekspe­ry­mentalnie. Kartezjusz za pomocą szczegółowych rachunków opartych na prawie załamania wykazał, że kąt, pod jakim widać tęczę – to po prostu kąt, pod jakim odbija się najwięcej światła (światło odbija się tu od wewnętrznej powierzchni kropel wody, por. ryc. 3). Obliczony kąt porównał Kartezjusz z obserwowanym, wykonując odpowiednie doświadczenie. Praca dotycząca tęczy jest wyjątkiem u Kartezjusza, który z czasem coraz bardziej skłaniał się ku wyprowadzaniu objaśnień fizykalnych z racjonalnych zasad bez oglądania się na niewygodne szczegóły. Prawdopodobnie byłby bardzo zaskoczony, gdyby dowiedział się, że z jego całej fizyki przetrwał tylko jeden fragment: wyjaśnienie tęczy.

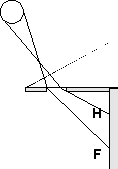Ryc. 4 Powstawanie barw w pryzmacie według Kartezjusza

Pragnąc objaśnić również barwy tęczy Kartezjusz przypomniał sobie, że podobne barwy obserwuje się w szklanym pryzmacie. Doświadczenie, które pouczyło go o przyczynach tych barw, opisał w Meteorach (ryc. 4). Światło słoneczne pada na pryzmat, za którym jest szczelina i dalej ekran. Jeśli szczelina jest „dość wąska”, to jej obraz na ekranie jest wstęgą barw od fioletu w H po czerwień w F. Ponieważ w doświadczeniu zachodzi tylko pojedyncze załamanie i nie ma odbicia, przeto należy wnioskować, że nie odbicie, lecz właśnie załamanie jest przyczyną pojawiania się kolorów tęczy. Ponadto z faktu, że barw takich nie obserwuje się w płaskich płytkach szkła (np. w szybach), należy wnioskować, iż musi być to załamanie nie skompensowane żadnym innym. Dalej: aby widzieć barwy, potrzebujemy światła (antyczne rozróżnienie wciąż się na­rzu­cało) i również cienia, czyli „ograniczenia światła” – bo gdy szczelina staje się szeroka lub gdy ją całkiem usuniemy, obraz ma postać białego pasa zabarwionego jedynie przy brzegach. Barwy pojawiają się zatem w obszarze sąsiadującym z cieniem na skutek załamania. Próbując wyjaśnić, dlaczego jeden brzeg obrazu jest fioletowo-niebieski, drugi zaś czerwono-żółty, Kartezjusz przyjmuje, że okrągłe cząstki eteru, które przekazują owo „działanie czy ruch”, jakim jest światło, mogą się obracać. Przy obu brzegach cienia ruch obrotowy nadawany cząstkom materii jest różny. Tam, gdzie obser­wuje się barwę czerwoną (wciąż uważaną za najsilniejszą), cząstki „dążą do obracania się z większą siłą niż do poruszania po linii prostej” (chodziło prawdopodobnie o prędkość obrotu większą niż ruchu postępowego, równe prędkości odpowiadałyby toczeniu się), barwie fioletowej (najsłabszej) odpowiada sytuacja odwrotna.

W rozumowaniu tym widać, jak Kartezjusz wyobrażał sobie osiąganie pewnych wyników w nauce za pomocą swej metody. Skoro światło jest tylko skłonnością do ruchu w materii, to nie potrzeba mnożyć bytów i osobno szukać objaśnienia barw i światła. Skoro zaś możliwe ruchy są postępowe lub obrotowe, a światło ma rozma­ite kierunki rozchodzenia się i barwy, to z konieczności barwy należy wiązać z obrotami.

Przy okazji Kartezjusz obalił rozróżnienie barw pozornych – takich jak barwy tęczy, i barw prawdziwych – takich jak barwy przedmiotów, które istnieją, jak wierzono, nawet w ciemności. U Kartezjusza wszystkie barwy stają się barwami pozornymi: nie tylko więc nie widzimy bezpośrednio samych przedmiotów, lecz jedynie wysyłane przez nie światło, ale również nie widzimy ich barw, lecz jedynie barwę światła wpadającego do naszych oczu.

Odkrycie i uzasadnienie ścisłego prawa załamania nastąpiło wtedy, gdy zaczęto poszukiwać matematycznych praw przyrody. Jak wykazał Boyer, znajomość starożytnej tabelki kątów załamania wys­ta­r­czyłaby do obliczenia promienia tęczy metodą Kartezjusza. Nikt jednak nie wykonał tych obliczeń przez półtora tysiąca lat, dopóki nie poznano prawa załamania i dopóki nie zaczęto myśleć w kate­go­riach ilościowych: tęczę widać w kierunku, z którego przychodzi najwięcej promieni. W ścisłość prawa załamania wierzono bardziej dzięki teoretycznemu uzasadnieniu niż dokładnym pomiarom. Prace optyczne Newtona miały oprzeć się na założeniu, że prawo zała­mania spełnione jest z absolutną dokładnością.