GEOMETRIA RUCHU

Co bowiem znajduje się w umyśle ludzkim oprócz figur i wielkości? Jedynie te rzeczy możemy poznać w sposób właściwy i – jeśli pobożność pozwala nam to powiedzieć – nasz sposób pojmowania jest w tym zakresie tego samego rodzaju co pojmowanie boskie.

Johannes Kepler

Największym osiągnięciem naukowym Izaaka Newtona miało być stworzenie matematycznej mechaniki i teorii grawitacji. Dzięki temu wiele na pozór nie związanych ze sobą odkryć poprzedników zostało połączonych w jedną całość, a prawa fizyki odkryte i zba­dane na Ziemi po raz pierwszy zastosowane były do objaśnienia budowy Wszechświata.

Uczeni XVII w. wyznawali filozofię mechanistyczną i chętnie mówili o świecie jako boskim zegarze. Wszelako szczegóły funkcjo­nowania tego zegara i zasady działania ziemskich zegarów nie miały wiele wspólnego.

W kosmologii wywodzącej się od Arystotelesa świat (a z nim cała fizyczna przestrzeń) miał kształt kuli i składał się z szeregu koncentrycznych sfer unoszących przytwierdzone do nich sztywno planety. Modelem był tu Księżyc, zwrócony do nas zawsze tą samą stroną. Najbardziej zewnętrzna sfera primum mobile nadawała ruch leżącej niżej sferze gwiazd stałych i ten ruch obrotowy przeka­zywany był kolejno w dół coraz niższym sferom aż do sfery Księżyca. W środku świata nieruchomo spoczywała Ziemia.

Starożytni Grecy pozostawili również szczegółową matema­tyczną teorię położeń planet, pozwalającą na przewidywanie zja­wisk astronomicznych w rodzaju zaćmień czy koniunkcji. Teoria ta zebrana została przez Klaudiusza Ptolemeusza w dziele znanym pod zniekształconą nazwą Almagest. Zamiast obracających się sfer astro­no­mia matematyczna używała konstrukcji złożonych z kół poru­szających się po kołach, aby niejednostajne ruchy planet rozłożyć na jednostajne ruchy koliste. Model geometryczny służyć miał do pra­ktycznych obliczeń i traktowano go jako formalne narzędzie, a nie opis rzeczywistości.

Reforma podjęta przez Kopernika nie zmieniała obrazu obra­ca­jących się sfer, o czym świadczy sam tytuł dzieła: O obrotach sfer niebieskich, zamieniała jedynie miejscami ciała centralne. Kopernik pragnął uzgodnienia modelu obracających się sfer z astronomią ma­te­matyczną. Kierował się przeświadczeniem, że tylko prawdziwe hi­potezy planetarne mogą być zgodne z obserwacjami.

Ukazanie się w roku 1543 dzieła Mikołaja Kopernika nie spowo­do­wało niemal żadnego widocznego skutku. Pierwszym wybitnym kontynuatorem i jednocześnie otwartym zwolennikiem jego teorii był dopiero Johannes Kepler, protestancki uczony, który począt­kowo zamierzał zostać duchownym, lecz poświęcił się astronomii. Skłoniło go do tego odkrycie podstawowej w jego mniemaniu zasa­dy architektonicznej Kosmosu. Zauważył on mianowicie, że propor­cje sfer poszczególnych planet mogą być określone geometrią foremnych wielościanów, tzw. brył platońskich: czworościanu, sześ­cianu, ośmiościanu, dwunastościanu i dwudziestościanu. Sfery planet miały być sferami opisanymi i wpisanymi w kolejne wieloś­ciany. Wyjaśniałoby to nie tylko wielkości, ale i liczbę planet – łącznie z Ziemią sześć – ponieważ istnieje tylko pięć foremnych wielościanów. Aby sprawdzić zgodność swej hipotezy z obser­wacjami, Kepler udał się do Pragi do Tychona de Brahe, najdok­ład­niejszego obserwatora w dotychczasowej historii astronomii, choć przeciwnika systemu kopernikańskiego. Hipoteza Keplera w pier­wotnym sformułowaniu nie odpowiadała danym obserwacyjnym, ale Kepler zdobył dostęp do wieloletnich obserwacji Tychona i za­czął szukać matematycznych prawidłowości w ruchu planet.

Praca Keplera była świadectwem zarówno pomysłowości teore­tycznej, jak i uporu w ścisłym dopasowywaniu wyników obliczeń i obser­wacji. Sprawdzenie każdego pomysłu wymagało bardzo wie­lu rachunków, które Kepler przeprowadzać musiał sam bez niczyjej pomocy. Zbawienna w skutkach rozbieżność zaledwie kilku minut kątowych spowodowała odrzucenie jednej z wersji teorii. Dla porów­­nania: zdolność rozdzielcza oka ludzkiego, która jest abso­lutną granicą dokładności obserwacji wykonywanych gołym okiem, wy­no­si około jednej minuty kątowej. Ostatecznie Kepler zbudował teo­rię ruchów planet dorównującą w dokładności obserwacjom Tychona.

Kepler pierwszy uznał Słońce nie tylko za gigantyczną lampę oś­wie­t­lającą świat, lecz także za źródło i centrum ruchu planet. Obserwacje komet prowadzone przez Tychona dowiodły, że ko­mety mogą swobodnie przenikać przez sfery planet – co ozna­cza­ło, że nie ma żadnych krystalicznych sfer unoszących planety. Nale­żało więc szukać innego wyjaśnienia ich ruchu. Planety poruszają się szybciej, gdy są bliżej Słońca, i wolniej, gdy są od niego dalej. To z kolei oznaczało, że gdyby każdą planetą kierowała rezydująca w Słońcu dusza poruszająca – anima motrix – to musiałaby ona słab­nąć bądź wzmacniać się zależnie od odległości planety od Słońca według pewnego sta­łego prawa matematycznego. Anima motrix musiałaby wykonywać obserwacje odległości i obliczać sto­sowne prędkości, być czymś w rodzaju komputera. Za bardziej naturalne uznał w końcu Kepler przypisanie Słońcu pewnej siły (vis) poru­szającej planety i działającej w płaszczyźnie orbity. Siła ta, rozcho­dząc się w płaszczyźnie, malałaby odwrotnie proporcjonalnie do odległości od Słońca. Kepler założył, że prędkość planety zmienia się tak samo jak siła (co jest nieprawdą). Stosując w swym rozumo­waniu jeszcze jedno nieprawdziwe twierdzenie ostatecznie otrzymał Kepler pra­wdziwą konluzję, znaną dziś jako II prawo Keplera. Głosi ono, że pola zakreślane przez promień wodzący planety w jednako­wych odstępach czasu są jednakowe (ryc. 17). Kepler ustalił rów­nież, że orbity planet są elipsami, w których jednym ognisku znaj­du­je się Słońce (I prawo Keplera). Niezależnie od wątpliwych uzasa­d­nień teoretycznych oba prawa dobrze pasowały do obserwacji.

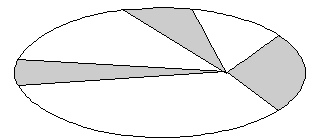Ryc. 17 Drugie prawo Keplera

Kepler jest twórcą układu heliocentrycznego, który znamy. Po­dob­nie jak Kopernik szukał on praw rządzących Kosmosem, a nie tylko metod pozwalających obliczać położenia planet na podstawie dowolnych założeń. Był on przekonany, że Bóg zrealizował w ukła­dzie planetarnym pewien ład matematyczny i przez całe życie po­szu­kiwał zasad, którymi kierował się Stwórca i które z woli Stwórcy mogą zostać przez ludzi w jakiejś części poznane, choć niektóre zagadnienia, np. sekret takiego, a nie innego rozmieszczenia gwiazd na ich sferze, pozostaną może na zawsze nie wyjaśnione. Wszechświat był dla Keplera obrazem Trójcy Świętej z nieru­cho­mym i rządzącym wszystkim Słońcem – odpowiadającym Ojcu, z nie­ruchomą sferą gwiazd stałych, która konstytuuje przestrzeń dla ruchu planet – odpowiadającą Synowi Bożemu i z poruszającą siłą Słońca, która wypełnia świat i odpowiada Duchowi Świętemu.

W późniejszych latach Kepler odkrył jeszcze jedno prawo doty­czące układu planetarnego: kwadraty okresów obiegu planet są proporcjonalne do sześcianów rozmiarów ich orbit. To łatwo spraw­dzalne prawo zyskało najszybciej uznanie i miało odegrać rolę w formułowaniu prawa ciążenia.

Dzieła Keplera trudne, dziwaczne, opisujące szczegółowo nie tylko ostateczne wyniki, ale i szczegóły wszystkich nieudanych po­my­s­łów ich autora, nie były nigdy akceptowane bez zastrzeżeń. Dla wielu, wśród nich Galileusza, nie do przyjęcia był keplerowski mistycyzm, łączący harmonię sfer, bryły platońskie i dynamikę nieba. Trwałym osiągnięciem okazały się prawa ruchu planet, będące pięknym i stosunkowo dokładnym przybliżeniem. Aż do czasu Newtona nie były jednak przyjmowane bez zastrzeżeń. Orbity planet są elipsami zbliżonymi do kół i niełatwo ustalić, czy rzeczy­wiście są elipsami, czy jakimiś innymi owalami. Ponadto II prawo – prawo pól – w praktycznych obliczeniach może być stosowane jedynie w przybliżeniu, a ponieważ jego podstawy teoretyczne były wątpliwe, rodziło to wątpliwości co do ścisłości samego prawa. Wielu astronomów zaniepokojonych pustym, nie odgrywającym żadnej roli drugim ogniskiem elipsy przyjmowało, że względem tego drugiego ogniska planeta porusza się jednostajnie, co w przy­bliżeniu daje te same wyniki. Dopiero w mechanice Newtona II prawo Keplera miało otrzymać teoretyczne uzasadnienie.

Kepler pierwszy potraktował ruch planet jako zagadnienie me­chaniki. Stosował do niego zasady fizyki Arystotelesa – jedyne jakie istniały. W filozofii Arystotelesa inne zasady rządzą niezmien­nym niebem, gdzie ruchy są kołowe, a materia niezniszczalna, inne natomiast w sferze podksiężycowej. Spośród czterech rodzajów zmian (czyli ruchu) rozróżnianych przez Arystotelesa najważniej­szym i najbardziej kłopotliwym okazał się ruch lokalny, tzn. zmiana położenia – to, co obecnie nazywamy po prostu ruchem. Arystoteles rozróżniał dwa rodzaje ruchu lokalnego: naturalny i wy­mu­szo­ny. Ruchem naturalnym był swobodny spadek kamienia lub wznoszenie się dymu do góry w bezwietrzną pogodę. Ruchy te były prostoliniowe i przyspieszone, skierowane do (lub od) centrum świata.

Oprócz ruchów naturalnych możliwe były też ruchy wymu­szo­ne, np. ruch kamienia rzuconego w górę. Ruch wymuszony był skut­­kiem działania siły i nadawał ciału prędkość proporcjonalną do tej siły oraz odwrotnie proporcjonalną do oporu ośrodka.

Szczególnie kłopotliwy był problem rzutów: co wprawia w ruch kamień wypuszczony już z ręki? Rozmaitość wyjaśnień podawanych w ciągu stuleci obowiązywania filozofii Arystotelesa świadczyła o bra­ku zadowalającego rozwiązania tej kwestii. Sam Arystoteles twier­dził, że powietrze otaczające rzucony kamień występuje w po­dwójnej roli – popycha go i jednocześnie stawia opór ruchowi.

W fizyce Arystotelesa wszelkie ruchy zachodziły w przestrzeni wypełnionej – próżnia była uważana za niemożliwą m.in. dlatego, że gdyby nic nie stawiało oporu, ruch ciał musiałby być natych­miastowy. W średniowieczu rozważano wprawdzie hipotetyczne ru­chy w próżni, lecz traktowano to jako ćwiczenie filozoficzne, a nie zagadnienie dotyczące przyrody. Podobnie zastanawiano się nad teoretyczną możliwością istnienia jakiejś przestrzeni na zewnątrz Kosmosu – kwestia ta stawiana była jedynie w kontekście całkowitej wolności Boga, który, gdyby zechciał, mógłby stworzyć i taką przestrzeń bądź wprawić w ruch cały istniejący świat.

Problemy ruchu były istotne dla wszystkich zwolenników teorii Kopernika. Przeciwnicy Kopernika utrzymywali, że ruch Ziemi miał­by widoczne i częstokroć dramatyczne skutki. Gdyby Ziemia się obracała, to np. kamień spadający ze szczytu wieży musiałby upaść daleko na zachód od stóp wieży: Ziemia bowiem ucieknie spod kamienia, zanim ten osiągnie Ziemię. Pilnym zadaniem zwolen­ników Kopernika stało się wykazanie, że na poruszającej się Ziemi wszystkie (lub niemal wszystkie) zjawiska będą przebiegać tak sa­mo, jak gdyby Ziemia była nieruchoma.

Decydujący postęp w nauce o ruchu dokonał się za sprawą Galileusza. Swoje badania w zakresie mechaniki podsumował on w dzie­le Rozmowy i dowodzenia matematyczne w zakresie dwóch nowych umiejętności ogłoszonym w roku 1638 w Holandii. Gali­leusz naśladował Archimedesa, który sformułował aksjomatycznie ujętą statykę. Do stworzenia matematycznej teorii ruchu niezbędna była idealizacja: Galileusz wprowadził do nauki świat, w którym ruchy odbywają się bez tarcia i oporu powietrza, a ciała można przedstawiać jako punkt geometryczny. Nie próbując wyjaśniać przyczyn swobodnego spadku dał jego wyczerpujący model mate­ma­tyczny. Ciało mogło brać udział w dwóch naraz ruchach: kamień upuszczony z wieży mógł jednocześnie spadać i poruszać się pozio­mo tak jak szczyt wieży. Jego ruch względem Ziemi był nadal pionowym spadkiem. U Galileusza ruch jest koncepcją geomet­ryczną, a nie stawaniem się czy rozwojem. Nie jest też stanem same­go ciała, lecz jest względny, zależy od ruchu obserwatora.

Ruch przestał być również przeciwieństwem spoczynku. Zasta­na­wiając się nad ruchem ciał staczających się z równi pochyłych o coraz mniejszym kącie nachylenia, których przyspieszenie (jak powiedzielibyśmy dzisiaj) jest coraz mniejsze, Galileusz doszedł do wniosku, że w granicznym przypadku poziomej gładkiej płaszczyz­ny ruch ciała stanie się jednostajny i prostoliniowy. Zatem ciało raz wprawione w ruch powinno poruszać się wiecznie, jeśli tylko zapew­­nimy mu owe idealne warunki. Ruch jest więc równie natu­ralny jak spoczynek i niekoniecznie wymaga podtrzymywania. Stwier­dzenie to – zasada bezwładności – odegrało kluczową rolę w budowaniu praw mechaniki.

Zasadę bezwładności Galileusz uogólnił twierdząc, że ciało po­ru­szające się swobodnie zachowywałoby stałą odległość od środka Ziemi, zataczając okrąg. Ruch po okręgu był zatem ruchem bez­władnym, nie wymagającym zewnętrznej siły do podtrzymywania. W taki właśnie sposób Galileusz, który nigdy nie był biegły w szczegółach astronomii matematycznej, wyjaśniał ruch planet wokół Słońca, przyjmując uproszczony model kopernikański z kołowymi orbitami. Model taki był niezgodny nie tylko z dokładnymi obser­wacjami Tychona, ale byłby nie do przyjęcia również dla samego Kopernika jako zbyt niedokładny.

Galileusz podał również własne wyjaśnienie przypływów i od­pły­wów morza. Zjawisko to, podobnie jak przyciąganie magnesu, zawsze należało do najtrudniejszych do objaśnienia. Bez żadnego widocznego powodu wody morskie na przemian przybierają bądź opadają dwa razy na dobę. Ponieważ każdy następny przypływ spóźnia się o ok. 30 min, tzn. mniej więcej o godzinę na dobę – tyle samo co dobowe opóźnienie Księżyca wywołane jego ruchem wśród gwiazd, przypływy łączono od starożytności z działaniem Księżyca. Wyjaśnienie takie trudne było do przyjęcia dla wszystkich racjonalistów odrzucających tajemne wpływy, w tym dla arysto­telików. Należało tu w dodatku nie tylko wyjaśnić oddziaływanie na odległość, ale również fakt, że okres przypływów jest dwa razy krótszy niż doba księżycowa: zatem Księżyc działa nie tylko wtedy, gdy znajduje się nad horyzontem, ale i wtedy, gdy jest pod nim ukryty.

Gdyby Ziemia poruszała się jedynie ruchem orbitalnym – równoważnym według Galileusza spoczynkowi – nie moglibyśmy za­ob­serwować żadnych zjawisk wywołanych jej ruchem. Ziemia wiruje jednak również wokół osi, wskutek czego jej całkowita pręd­kość zmienia się: czasem prędkość związana z wirowaniem dodaje się do prędkości orbitalnej, a czasem od niej odejmuje. W wyniku tej nierówności woda mórz zachowuje się jak woda w naczyniu, na przemian poddawanym przyspieszaniu i spowalnianiu. Według tej teorii prawdziwy okres pływów nie ma oczywiście nic wspólnego z dobą księżycową.

Spekulacje dotyczące przypływów są centralną i najważniejszą częś­cią Dialogu o dwu najważniejszych układach świata ptoleme­uszowym i kopernikowym. Galileusz wyśmiewa tam wszystkich, którzy (jak Kepler) wiążą zjawisko przypływów z działaniem Księżyca:

Zdaję sobie sprawę, że ruch mórz jest miejscowy i że dostrzega się go łatwo w olbrzymich masach wód, toteż nie mogę pogodzić się z przypi­saniem go wpływom jakiegoś światła, jakiejś umiarkowanej ciepłoty, jakichś dominujących wpływów tajemnych i innym podob­nym złudnym wyobrażeniom, które tantum abest [tak są odległe od tego] by były lub mogły być przyczyną przypływu; na odwrót: przy­pływ jest przyczyną tych pomysłów i napędza je do ich mózgów, skłonniejszych do gadulstwa i samo­chwalstwa niż do rozważania i ba­da­nia najbardziej tajemnych poczynań przyrody [19].

Dla unikającego spekulacji, trzeźwego Galileusza wyjaśnienie przy­pływów działaniem na odległość było niedorzeczne. Prze­ciwnie, nie potrafiąc znaleźć żadnej bezpośrednio działającej przy­czy­ny, uznał, że tylko ruch Ziemi może wytłumaczyć owe zjawiska. Argument z przypływów miał być rozstrzygającym dowodem za słusznością teorii Kopernika i był jednym z głównych motywów publikacji Dialogu, który przyniósł tyle sławy i upokorzeń swojemu autorowi.

Dzisiejszą postać zasadzie bezwładności nadał dopiero Kar­tezjusz. W jego ujęciu ruch prostoliniowy i ruch kołowy są zasadni­czo różne. Pierwszy jest ruchem podtrzymywanym przez Boga, ruchem, który nie potrzebuje żadnej przyrodzonej przyczyny, aby trwać. Jest zatem z punktu widzenia fizyki ruchem bezwładnym. Inaczej natomiast przedstawia się sprawa ruchów kołowych. Klasycznym przykładem stał się tu kamień obracający się na sznur­ku jak w procy. Kamień ten stale wywiera działanie odśrodkowe, usiłując oddalić się od centrum swego ruchu po linii prostej sty­cznej do okręgu.

Jedyny rodzaj oddziaływania ciał w wypełnionym świecie Kar­tezjusza polegał na zderzeniach cząstek, w których nie zmienia się całkowita ilość ruchu. Ilość ruchu zależała od wielkości ciała oraz jego prędkości. Pojęcie to nie obejmowało kierunku – ilość ruchu po­zostawała taka sama, jeśli zmianie kierunku nie towarzy­szy­ła zmia­na wartości prędkości. Choć prawa zderzeń Kartezjusza oka­zały się błędne, problem zderzeń był podjęty przez następne po­kolenie uczonych i rozwiązany przez Wallisa, Huygensa, Mariotte'a, a także niezależnie od nich przez młodego Newtona.

Fizyka Kartezjusza nie miała jednak charakteru ilościowego, była bliska jakościowej tradycji arystotelesowskiej, dążyła do zrozu­mienia istoty zjawisk, podania ich filozoficznych przyczyn, a nie samego tylko opisu. Kartezjusz nie cenił abstrakcyjnych modeli matematycznych, chciał, aby filozofia objaśniała nie jakieś wyide­ali­zowane, sztuczne sytuacje w rodzaju tych rozważanych przez Galileusza, lecz aby pozwalała pojąć realne zjawiska w ich na­turalnym przebiegu.

Ambicje filozoficzne Kartezjusza obejmowały objaśnienie całości zjawisk przyrody ożywionej i nieożywionej – zarówno Wszech­świat, jak i wszystko, co się w nim znajduje, cały świat cielesny i roz­ciąg­ły można opisać jako maszynę, stosując do niego zasady filozofii. W szczególności Kartezjusz zastosował swoje zasady do Kosmosu i sfo­r­mułował teorię jego funkcjonowania – teorię wirów. W przeci­wieństwie do koncepcji Keplera teoria wirów zdo­by­ła ogromny rozgłos i była powszechnie przyjmowana aż do wy­parcia jej przez teorię grawitacji.

Według Kartezjusza materia niebios jest płynna i porusza się ruchem wirowym, podobnym do wirów na rzece. Układ Słoneczny jest ogromnym wirem, w którym utworzyło się kilka mniejszych wi­rów wokół niektórych z planet głównych. W tych mniejszych wirach krążą satelity planet. Wszystkie ruchy wirowe, łącznie z ob­ro­tem  planet wokół własnych osi, zachodzą więc w tym samym kierunku, zgodnie z tym, co się obserwuje. Osie tych wszystkich obrotów i obiegów są w przybliżeniu równoległe. Podobnie jak w przypadku wirów wodnych ruch planet nigdy nie zachodzi po doskonałych kołach za przyczyną wielu nierówności kształtu i ru­chu wiru oraz wirów sąsiednich. Każdy, kto obserwował wiry na rzece, nie będzie oczekiwał w przebiegu tych zjawisk ścisłych mate­ma­tycznych regularności. Kartezjusz przedstawił zresztą kilka kon­kretnych przyczyn nierówności ruchu planet. W jego teorii znacznie trudniej było zrozumieć, dlaczego ruch planet miałby podlegać jakimkolwiek ścisłym prawom.

Teoria wirów napotykała również trudności szczegółowe, gdy próbowano uzgodnić ją z wiedzą astronomiczną. Eliptyczność orbit tłumaczono ciśnieniem sąsiednich wirów, Merkury jednak, planeta najbardziej wewnętrzna, ma orbitę wydłużoną bardziej niż inne planety. Inną trudnością było wyjaśnienie, dlaczego planety nie poruszają się w płaszczyźnie równika słonecznego.

Ruch traktował Kartezjusz jako względny. Dzięki temu uchylił się od zajęcia stanowiska w niebezpiecznej kwestii, co jest nieru­chome: Ziemia czy Słońce. Każde z ciał niebieskich spoczywać mia­ło względem otaczającej je materii, przez którą jest unoszone – Ziemia porusza się więc nie bardziej niż śpiący pasażerowie statku płynącego z Calais do Dover.

Kartezjusz wyobrażał sobie, że świat w obecnej postaci tak czy inaczej musiałby powstać w wyniku działania praw przyrody. Jeśli założyć (nie upierając się, że istotnie tak było: zaprzeczalibyśmy bowiem księdze Genesis), że w pewnej chwili na początku cząstki materii były jednakowe co do rozmiarów i ruchu, to z czasem ich ruch i wielkości musiały zróżnicować się tak, jak to obserwujemy obecnie.

W fizyce Kartezjusza pojawiło się też wyjaśnienie ciężkości. Tradycyjnie uważano ciężkość (i lekkość) za przyrodzoną właści­wość ciał. Kartezjusz konsekwentnie nie przyjmował innych właści­woś­ci niż rozciągłość i ruch, musiał więc grawitację wyjaśnić w ję­zy­ku swojej filozofii. Podobnie jak wciąganie cieczy do opróżnionej ru­ry barometru wyjaśniono ciśnieniem atmosferycznym z zewnątrz, rów­nież przyciąganie ziemskie można było objaśnić popychaniem ze strony eteru. Kartezjusz przyjmował, że cząstki eteru wirując wo­kół Ziemi oddalają się od niej. Małe cząstki eteru przenikać miały przez większe cząstki pozostałej materii, które za nim nie nadążały. W rezultacie eter popychał grubsze cząstki w dół, ku Ziemi. Jak szyb­­­ko zauważyli krytycy, w myśl teorii Kartezjusza ciała powinny spa­dać prostopadle do osi obrotu Ziemi, a nie w kierunku jej środka.

Kartezjusz podał również swoje wyjaśnienie przypływów. Również on odrzucał działanie na odległość. Przyjął więc, że Księ­życ dzięki swoim rozmiarom odsuwa lekko Ziemię poza środek jej wiru, co powoduje ściskanie materii znajdującej się po przeciwnej do Księżyca stronie Ziemi. W rezultacie morza przybierają kształt spła­sz­czony, ubywając na linii łączącej Ziemię z Księżycem, a przy­bie­rając w kierunku do niej prostopadłym. Zgodnie z tą teorią należy oczekiwać przypływu w mniej więcej sześć godzin po góro­wa­niu (lub dołowaniu) Księżyca, co na wielu wybrzeżach jest prawdą.

Filozoficzne zasady Kartezjusza można było łączyć z uprawia­niem matematycznej mechaniki, jak czynił to Christiaan Huygens. Zastosował on metody Galileusza do wielu zagadnień szczegó­łowych. Mechanika u Huygensa stała się dziedziną specjalistyczną, stosującą zaawansowane metody matematyczne daleko wykra­czające poza elementarną geometrię.

Huygens unikał pojęcia siły. Zagadnienia dynamiki formułował w taki sposób, aby się bez tego pojęcia obywać. Stosował uogól­nioną przez siebie zasadę Torricellego, która mówiła, że środek ciężkości dowolnego układu ciał nie może się samorzutnie pod­nieść. Zasada ta jest równoważna zasadzie zachowania energii mechanicznej. Inną stosowaną przez Huygensa zasadą była zasada względności ruchu. Korzystając z niej odkrył on prawa rządzące zderzeniami sprężystymi.

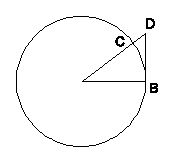Ryc. 18 Siła odśrodkowa według Huygensa

Sformułował w ten sposób prawdziwe prawa zderzeń zamiast fałszywych Kartezjańskich. W szczególności okazało się, że ilość ruchu, która była u Kartezjusza wielkością stałą, nie była zachowy­wana w zderzeniach. Huygens nie sformułował nigdy zasady za­cho­wania pędu, która zastępowałaby Kartezjańską stałość ruchu. Używał jednak równoważnej zasady stałości ruchu środka masy.

W związku z pracą nad zegarem wahadłowym (którego prototyp przed­stawił Huygens holenderskim Stanom Generalnym w ro­ku 1657) Huygens studiował zagadnienie ruchu po okręgu. Zaga­d­nie­nie postawione kiedyś przez Kartezjusza Huygens sformułował jako problem geometryczny. Gdyby uwolnić w pewnej chwili ciało poruszajace się jednostajnie po okręgu, to zaczęłoby ono oddalać się po linii prostej stycznej do tego okręgu (ryc. 18). Dla krótkiego cza­su wielkość tego oddalenia CD byłaby proporcjonalna do kwad­ra­tu długości łuku BC, a zatem i do kwadratu czasu – tak samo jak w swobodnym spadku rozważanym przez Galileusza. Huygens obli­czył, jak wielkość siły odśrodkowej zależy od prędkości ciała i pro­mienia okręgu.

Choć w zagadnieniu ruchu po okręgu Huygens mówił o sile, nie oznacza to, że traktował siłę jako przyczynę ruchu. Siła odśrod­kowa była raczej statyczną siłą naprężenia sznura procy i skutkiem ruchu obrotowego. Powszechnie używano wówczas pojęcia „siła” w znaczeniu „siła poruszającego się ciała”; jak w języku potocznym mówi się, że jakieś ciało pędziło lub uderzyło w coś z wielką siłą – mając na myśli, że poruszało się z dużą szybkością lub było duże.

Spuścizna, jaką otrzymał Newton po swoich poprzednikach, była bardzo niejednolita. Z jednej strony była to jakościowa fizyka Kartezjusza oparta na fantastycznej mechanice, z drugiej zaś – formalna astronomia matematyczna oraz ziemska mechanika ogra­niczona do wąskiej klasy problemów dotyczących wahadeł, zderzeń i spadania ciał, czyli zagadnień badanych jeszcze przez Galileusza.