OD ELIPTOIDY DO ELIPSY

W latach siedemdziesiątych Newton niemal wcale nie zajmował się mechaniką, wracał do niej tylko pod wpływem jakiegoś bodźca z zewnątrz. Tak było, gdy otrzymał traktat Huygensa i udowodnił niek­tóre jego twierdzenia swoimi metodami. Stosowane przez Huygensa podejście, wykorzystujące symetrie i unikające sformuło­wań dynamicznych, było jednak Newtonowi obce.

Pod koniec 1679 roku Newton otrzymał list od Hooke'a, który po śmierci Oldenburga został sekretarzem Towarzystwa Królew­skiego. List zaczynał się niezbyt fortunnym zwrotem: „stwierdziwszy w naszych Rejestrach, że podobał Pan sobie w korespondencji z Oldenburgiem”, i zawierał propozycję nawiązania korespondencji „filozoficznej”. Hooke chciał poznać opinię Newtona na temat swo­jej teorii ruchu planet oraz teorii sprężystości powietrza.

W odpowiedzi Newton zapewnił Hooke'a, że pożegnał się z filozofią, na którą szkoda mu czasu, i że nie zna jego hipotezy (co nie było prawdą). Zaproponował również, jakby od niechcenia, doświadczenie, które mogłoby wykazać ruch wirowy Ziemi.

Chodziło o znany problem kamienia swobodnie spadającego z wysokiej wieży. Newton zwrócił uwagę, że szybkość obracania się wierzchołka wieży jest większa niż jej podnóża i dlatego upusz­czony kamień będzie miał większą prędkość w kierunku wschod­nim niż punkt u podnóża wieży. Kamień wyprzedzi więc punkt podnóża wieży i odchyli się nieco, ale w kierunku wschodnim – odwrotnie, niż przewidywali przeciwnicy ruchu Ziemi. Zdając sobie sprawę z małości tego efektu obmyślił specjalne środki ostrożności, aby wykryć zjawisko.

Przy okazji stwierdził, że gdyby spadające ciało mogło po osiąg­nię­ciu powierzchni Ziemi nadal spadać swobodnie, to po zatocze­niu spirali spadłoby na centrum Ziemi. Spadanie do centrum Ziemi było jeszcze jednym klasycznym tematem akademickich rozważań już w średniowieczu. Wielu autorów spierało się, czy ciało takie zatrzymałoby się w środku Ziemi, czy też powracałoby po pewnym czasie do jej powierzchni.

Łamiąc daną w swym liście obietnicę dyskrecji Hooke odczytał odpowiedź Newtona na posiedzeniu Towarzystwa i nie omieszkał pu­b­licznie wytknąć mu błędu: ciało spadające swobodnie będzie na przemian zbliżać się do centrum i wznosić do powierzchni Ziemi, zakreślając całkiem inną krzywą niż spirala, „rodzaj eliptoidy” – jak ją określił.

Nie trzeba dodawać, że przyłapanie na błędzie zirytowało moc­no Newtona. W miarę upływu lat starał się zminimalizować przyczy­nę zajścia i trzydzieści lat później w jego opowiadaniach spirala stała się niedbałym pociągnięciem pióra, które Hooke wziął za spi­ralę. W odpowiedzi teraz z kolei Newton poprawił Hooke'a: tor nie będzie zamkniętym owalem, lecz bardziej skomplikowaną figurą o kształcie rozety, czymś w rodzaju obracającej się elipsy. Jeśli bo­wiem przyjąć, że grawitacja pozostaje stała pod powierzchnią Ziemi, to ciało będzie „krążyć kolejno wznosząc się i spadając za przyczy­ną swej siły odśrodkowej oraz ciężkości na przemian prze­ważających jedna nad drugą”.

W odpowiedzi Hooke stwierdza, że nie zakładał, aby grawitacja była stała. Przypuszcza raczej, że przyciąganie jest odwrotnie propor­­cjonalne do kwadratu odległości od centrum. Nie chodzi mu też o hipotetyczne ciało pod powierzchnią Ziemi – tam przyciąganie musiałoby maleć – lecz o ruch planet.

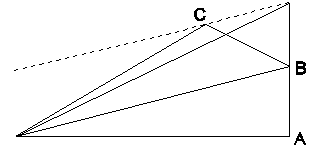Ryc. 20 Wyprowadzenie prawa pól

Hooke znał tylko elementarną matematykę i nie potrafił zwery­fikować swojej hipotezy. Próbował eksperymentować na modelach, ale ostatecznie niczego pewnego nie ustalił. Dla Newtona cenna oka­­za­ła się nie tyle sama hipoteza o przyciąganiu i prawie odwrotnych kwadratów (które wiele lat wcześniej wyprowadził z III pra­wa Keplera), ile sformułowanie problemu ruchu planet. Dotąd wyobrażano sobie ruch krzywoliniowy jako rodzaj równowagi: ide­al­­nej przy ruchu kołowym, naruszonej przy ruchu eliptycznym. Hooke zaproponował znaczne uproszczenie pojęciowe: ruch krzywo­­­liniowy miał być rezultatem działania jednej tylko siły przy­ciągania. Pod jej działaniem tor planety byłby stale zakrzywiany do wewnątrz.

Newton nie odpowiedział Hooke'owi, zaczął jednak zastanawiać się nad nową koncepcją ruchu. Jak zwykle u Newtona oznaczało to budowanie matematycznej teorii. Tak jak kiedyś starał się zmatema­tyzować zagadnienia zderzeń i siły odśrodkowej kluczowe dla me­cha­niki kartezjańskiej, tak teraz nadał matematyczny kształt jakoś­ciowym rozważaniom Hooke'a. Sformułował trzy „hipotezy” – założenia dotyczące zasad ruchu. Pierwsza była prawem bez­władności, druga mówiła, że „zmiana ruchu jest zawsze propor­cjonalna do siły, przez którą [ruch] jest zmieniany”, trzecia wreszcie była zasadą równoległoboku w odniesieniu do składania ruchów.

Opierając się na tych zasadach udowodnił kilka twierdzeń. Pierwsze z nich głosiło, że jeśli siła działa stale w kierunku pew­nego centrum, to w ruchu ciała obowiązuje prawo pól, tzn. II pra­wo Keplera. Aby to wykazać, Newton traktował działanie siły przy­ciagającej jako ciąg impulsów w równych odstępach czasu popy­chających ciało ku centrum. Tor ABC takiego ciała byłby wtedy linią łamaną (ryc. 20). Pola zakreślane między kolejnymi impulsami są jednakowe, co łatwo udowodnić za pomocą elementarnej geo­metrii. Jeśli wyobrazimy sobie następnie, że impulsy stają się coraz częstsze, tor będzie przybliżał się do ciągłej krzywej, a prawo pól nadal pozostanie słuszne.

Następne twierdzenie dotyczyło ruchu po elipsie. Załóżmy, że ciało porusza się po elipsie zgodnie z prawami Keplera. Jak siła, która wywołuje ten ruch, zależy od odległości od centrum? Najprost­szą sytuację mamy dla dwóch skrajnych punktów elipsy: naj­bliż­szego i najdalszego od centrum siły. W obu punktach, gdyby nie przy­ciąganie, ciało poruszałoby się po linii prostej stycznej do eli­psy. Pod wpływem przyciągania ciało odchyla się od stycznej. Aby porównać siły przyciągania w obu punktach, należy porównać od­chy­lenia od stycznej dla jednakowego, krótkiego czasu (ryc. 21). Geometria problemu jest taka sama jak w rozważaniach Huygensa (por. ryc. 18) i łatwo stwierdzić, że odchylenia te są proporcjonalne do kwadratów prędkości ciała w obu punktach. Prędkości te są zaś, zgodnie z II prawem Keplera, odwrotnie proporcjonalne do odleg­łoś­ci obu punktów od centrum siły. Wobec tego siły przyciągające są w odwrotnym stosunku kwadratów odległości.

Twierdzenie to Newton uogólnił dalej na dowolny punkt keple­row­skiej elipsy. W ten sposób udowodnił, że ruch keplerowski za­cho­dzi pod działaniem przyciągania odwrotnie proporcjonalnego do odległości. Rozważania te miały stanowić przełom w wyjaśnianiu me­chaniki układu planet i później znalazły się w Principiach. Na razie jednak Newton nie stosował ich do planet, lecz traktował ra­czej jako ćwiczenie matematyczne i na kilka lat znowu przestał zaj­mować się mechaniką.

W kolejnym liście Hooke doniósł o doświadczalnym potwier­dzeniu efektu przewidzianego przez Newtona. Sukces doświad­czenia był pozorny – przy spadku z wysokości 9 m w ekspery­mencie Hooke'a odchylenie wynosi tylko około 0,3 mm – mniej, niż można było wykryć ówczesnymi technikami. Newton nie odpo­wiedział na ten list. Nie pokazał również nikomu swoich twier­dzeń o ruchu eliptycznym.

Pod koniec roku 1680 w całej Europie obserwowano wyjątkowo jasną kometę, która stała się powodem całej fali publikacji i dys­kusji. 1 stycznia 1681 r. „Journal des Sçavants” pisa³:

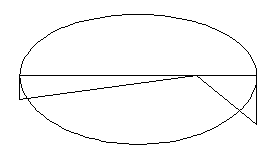Ryc. 21 Zależność siły od odległości w ruchu keplerowskim

Wszyscy mówią o komecie. Stanowi ona niewątpliwie najbardziej godne uwa­gi wydarzenie początku tego roku. Astronomowie śledzą jej tor, a lud uwa­ża ją za przepowiednię tysięcy nieszczęść; cyt. w [24].

Uczeni nie podzielali opinii tłumu. W wydanych z okazji komety Pensées diverses Bayle potraktował lęk przed kometami jako zjawis­ko społeczne i historyczne. Dlaczego z powodu śmierci jakiegoś kró­la miałaby się ukazywać na niebie kometa? Bayle uważa, iż tylko ludzka próżność mogła podsunąć myśl tak absurdalną – to jakby uznać kobietę wyglądająca przez okno na ulicy Saint-Honoré za przy­czynę przejeżdżania tamtędy powozów. Sceptyk Bayle i poboż­ny Newton zgodziliby się obaj, że powszechna opinia znaczy niewiele i kształtowana jest przez pełną przesądów większość.

W obaleniu wiary w prognostyczną funkcję komet miały swój udział osiągnięcia astronomii. Aż do XVI w. sądzono, że komety, po­dobnie jak chmury, tęcza i meteory, należy zaliczyć do zjawisk „meteorologicznych” zachodzących w sferze podksiężycowej. Dopiero Tycho de Brahe wykazał pomiarami, że kometa z 1577 r. znajduje się dalej niż Księżyc. Mimo tak wielkiej odległości warko­cze komet mogą rozciągać się na niebie na wiele stopni. Oznaczało to, że są one dużo większe niż cała Ziemia, nie mówiąc o królest­wach czy miastach na jej powierzchni.

Pojawiła się kwestia określenia toru zakreślanego przez komety i Tycho de Brahe oraz Maestlin, nauczyciel Keplera, próbowali go obliczyć dla komety z 1577 r. Obaj zakładali orbitę kołową. Nieuda­ne próby wyjaśnienia ruchu komety na podstawie układu Ptolemeusza spowodowały, że Maestlin przekonał się do koperni­ka­nizmu, który zaszczepił Keplerowi. Sam Kepler sądził, że ruch komet powinien odbywać się po liniach prostych, ponieważ nie obserwuje się, aby był on okresowy. Heweliusz przypuszczał, że komety poruszają się po parabolach – jak rzucone ciała w teorii Galileusza. Większość astronomów, jak Wren, Auzout i Cassini, uważała ruch komet za prostoliniowy, choć Cassini szukał danych na temat ewentualnych powrotów tych samych komet w pobliże Słońca.

Jeśli nawet uczeni nie wierzyli w związek komet z lilipucimi wydarzeniami na Ziemi, to mimo wszystko narzucało się pytanie o rolę, jaką spełniają w świecie te gigantyczne i efemeryczne ciała. Zawsze prozaiczny Kartezjusz chciał w nich widzieć zabłąkane pla­nety, rodzaj kosmicznych odpadków. Newton miał im przypisać zna­cz­nie szlachetniejszą funkcję w Bożym planie.

Zainteresowanie Newtona kometą 1680 r. było wyjątkowo żywe. Pomimo swej krótkowzroczności sam prowadził obserwacje komety przez wklęsłą soczewkę używaną jako monokl, a potem przez lu­netę. Zbierał informacje od innych obserwatorów. Mierzył również położenia komety mikrometrem „zbudowanym dość prymitywnie”, lecz pozwalającym na pomiar z błędem nie przekraczającym jednej minuty kątowej. Kometę widziano najpierw do przejścia przez perihelium i później po kilku tygodniach ponownie. Powszechnie sądzono, że są to dwie różne komety. Odmienną opinię wypo­wiadał Królewski Astronom John Flamsteed, który miał własną te­o­rię jej ruchu. Kometa miała być unoszona w słonecznym wirze i jed­no­­cześnie przyciągana do Słońca, a następnie od niego odpy­cha­na siłą magnetyczną. W rezultacie miała zakreślać tor zwrócony wy­pukłością ku Słońcu (ryc. 22).

W nie wysłanym liście do Flamsteeda Newton argumentował, że w żadnej chwili prędkość komety nie może być skierowana do Słońca, ponieważ przyciągana przez Słońce musiałaby na nie spaść po linii prostej. Z tego powodu krzywa Flamsteeda jest nie do przy­jęcia. Jedyny możliwy tor zbliżania się i oddalania od Słońca to linia krzywa obejmująca Słońce (ryc. 23). Ponadto

choć mogę łatwo dopuścić moc przyciągającą w Słońcu, dzięki której planety powstrzymywane są w swym biegu od oddalenia się od niego wzdłuż linii stycznych, to jednak mniej skłonny jestem przypuścić, że owo przyciąganie jest natury magnetycznej, ponieważ Słońce jest ogrom­nie gorącym ciałem, a ciała magnetyczne rozgrzane do czerwoności tracą swe zdolności [43].

W odróżnieniu od swych uczonych kolegów Newton nieskłon­ny był przypisywać Słońcu jakiegoś innego, odmiennego rodzaju mag­netyzmu niż ten znany na Ziemi, a ziemskie magnesy istotnie tra­cą swe właściwości po ogrzaniu.

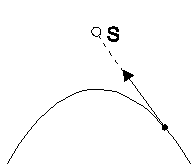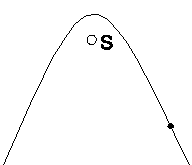Ryc. 22 Ruch komety wg Flamsteeda	Ryc. 23 Ruch komety wg Newtona

W liście tym zarówno opis ruchu­ jako odchylania od linii prostej, jak i opis ruchu przez siłę odśrodkową równoważącą się z siłą przyciągania występują razem – świadcząc o pojęciowym zamie­szaniu, z którego sam Newton nie zdawał sobie chyba jasno sprawy. Choć gotów był rozważać przy­ciągającą zdolność Słońca, to nie łączył jej z ruchem planet, tak jak nie odnosił do ruchu planet i ko­met swoich niedawno udowod­nionych twierdzeń. Newton bronił też w wysłanej ostatecznie wersji listu poglądu, że komety były dwie, co dodatkowo świadczy o jego wahaniach w tym okresie.

Rękopisy wskazują, że próbował dla komety lat 1680–1681 znaleźć prostoliniowy tor na podstawie czterech obserwacji, korzys­tając z wymyślonej przez siebie metody. Być może niepowodzenie tych obliczeń wpłynęło na późniejszą zmianę poglądu i przyjęcie orbity zakrzywiającej się wokół Słońca.

Kilka następnych lat nie przyniosło żadnych niemal wyników do­ty­czą­cych ruchu. Sytuacja wydaje się z perspektywy czasu para­doksalna: Newton dysponował wszystkimi elementami potrzebnymi do stworzenia matematycznej teorii ruchu planet i komet, a jednak wszystkie te elementy wciąż istniały oddzielnie, nie łącząc się w żadną całość.

powrót do strony głównej