GRAWITACJA

pozostaje nam objaśnić system świata za pomocą tych zasad [...]

I. Newton, Wstęp do III księgi Principiów

W tym samych przełomowych latach 1684-1685, gdy powstawały zasady mechaniki, Newton pisał wielokrotnie do Flamsteeda, pro­sząc go o dane na temat satelitów Jowisza, pozycje paru gwiazd w gwiazdozbiorze Perseusza (blisko których przeszła kometa w roku 1680, jak łatwo domyślił się Flamsteed), informacje dotyczące ko­niun­kcji Jowisza i Saturna oraz przypływów morza. Zestawienie tematów wskazuje na pracę nad teorią grawitacji. Podczas rozmowy z Halleyem w 1684 r. Newton jeszcze nie myślał o powszechnym ciążeniu. W trakcie pracy w ciągu roku 1685 stopniowo wyjaśniało się, że teoria powszechnego ciążenia nie tylko zgadza się z obser­wacjami, lecz może również w jednolity sposób objaśnić zjawiska, których związku nawet nie podejrzewano.

Teoria grawitacji, przedstawiona w III księdze Principiów, jest ukoronowaniem osiągnięć naukowych Newtona. Odkąd przestano wierzyć, że planety są unoszone przez sfery niebieskie, pojawiło się pytanie, co utrzymuje układ planetarny w ciągłym i regularnym ru­chu. Możliwej odpowiedzi dostarczała teoria wirów: świat jest wy­pe­ł­niony materią tworzącą wiry, w których poruszają się (a właści­wie „pływają”) planety. Ścisłe regularności ich ruchów miały zna­cze­nie drugorzędne wobec „filozoficznego”, jakościowego, objaś­nie­­nia przyczyn, które sprawiały, że świat tak właśnie wyglądał.

Koncepcja Newtona była całkowicie odmienna. Przede wszyst­kim planety poruszają się w próżni, a przynajmniej w eterze tak rozrzedzonym, że nie stawia on żadnego oporu ich ruchowi. Ruch planet jest więc znakomitym przykładem zastosowania praw mecha­niki matematycznej. Gdyby nie grawitacja, planety poruszałyby się owym idealnym ruchem jednostajnym i prostoliniowym, o którym mówi się w I prawie, ale który na Ziemi trudno zaobserwować. Wskutek działania siły grawitacji tory planet są co prawda zakrzy­wione, lecz zakrzywienie to podlega ścisłemu prawu matema­ty­cznemu. Zamiast spekulować na temat przyczyny ruchu planet, moż­­na po prostu obliczać ich położenia.

Aby jednak wykonać takie obliczenia, należało pokonać ogrom­ne trudności matematyczne. Siły powodujące ruch zależą od po­łożenia ciał przyciągających, które na ogół też się poruszają. Już za­ga­d­nie­nie dwóch przyciągających się ciał jest dużo trudniejsze ma­te­ma­ty­cznie niż wszystkie problemy rozważane przez Galileusza. Dla trzech ciał przyciągających się według prawa odwrotnych kwadra­­tów nie można w ogóle uzyskać rozwiązań ogólnych i Newton (jak i wszys­cy po nim) zmuszony był uciekać się do me­tod przybli­żo­nych.

Teoria Newtona również tym się różniła od osiągnięć poprzed­ników, że miała być słuszna dla wszystkich ciał we wszystkich okolicznościach, zawsze i wszędzie. Po raz pierwszy prawa odkryte na Ziemi zastosowane zostały do całego znanego Kosmosu. Co więcej, z punktu widzenia Newtona Wszechświat był jedynie szcze­gólnym przypadkiem jego matematycznej „filozofii”. Bez przesady można stwierdzić, że właśnie w tym momencie narodziła się fizyka matematyczna.

Do trudności matematycznych dołączały się trudności poję­ciowe. Filozofom wychowanym na Kartezjuszu podejrzane wydawa­ło się już samo pojęcie siły jako przyczyny ruchu, a co dopiero siły  – w dodatku przyciągającej – działającej na odległość poprzez próżnię. Chcąc uniknąć krytyki Newton starał się przedstawić swą teorię jako nieodparte połączenie wyników obserwacji z rozumo­waniami matematycznymi. Dlatego najpierw przedstawił swe za­łożenia metodologiczne:  słynne reguły rozumowania – Regulae philo­so­phandi. Następnie, stosując matematyczne wyniki dwóch pierwszych ksiąg, wyprowadził z faktów obserwacyjnych prawo grawitacji oraz omówił jego rozmaite konsekwencje. Sprowadzenie dyskusji nad filozoficznie kontrowersyjną teorią na grunt matema­tycznych dowodzeń było taktyką zastosowaną niegdyś przez Kopernika, on również ogłaszał teorię wywrotową w stosunku do uznanej wiedzy.

W ostatecznej wersji z III wydania Principiów reguły rozu­mo­wania przedstawiają się następująco:

I Nie należy przyjmować przyczyn rzeczy przyrodzonych w większej licz­bie, niż to jest zarówno prawdziwe, jak i wystarczające do objaś­nienia zjawisk.

II Dlatego tym samym skutkom przyrodzonym musimy, jeśli to możliwe, przypisywać te same przyczyny.

III Jakości ciał, które nie dopuszczają stopniowanego nasilenia ani osła­bienia i które przysługują wszystkim ciałom w zasięgu naszego doś­wiad­czenia, należy uznać za powszechne jakości wszystkich ciał. 

IV W filozofii eksperymentalnej należy uważać twierdzenia wyprowa­dzone za pomocą indukcji ogólnej ze zjawisk za prawdziwe lub bar­dzo bliskie prawdy, pomimo jakichkolwiek hipotez przeciwnych, które można by sobie wyobrazić, aż do czasu, gdy zajdą inne zjawiska i poz­wolą je [twierdzenia] albo bardziej uściślić, albo uznać za dopusz­czające wyjątki [47, 49, 51].

 

Reguła I, newtonowska wersja brzytwy Ockhama, wyraża pow­sze­chne wtedy przekonanie o ekonomii działań Stwórcy, która po­win­na znaleźć swoje odbicie w naszych teoriach. Regułę II ilustruje Newton przykładami: takie same przyczyny powinniśmy przypisać

oddychaniu człowieka i zwierząt, spadkowi kamienia w Europie i w Ame­ryce, światłu ognia ziemskiego i słonecznego, odbiciu światła na Ziemi i na planetach [47, 49, 51].

Przykładem jakości powszechnej, do której stosuje się III reguła, jest rozciągłość. Doświadczenie poucza nas, że wszystkie znane ciała są rozciągłe, więc jakość rozciągłości przysługiwać musi ciałom powszechnie. Podobnie obserwujemy, że ciała są twarde, skąd  wnio­s­kujemy, że twardość przysługiwać musi również pojedyn­czym, niewidocznym cząstkom, z których składają się te ciała. Podobnie ma się rzecz z nieprzenikliwością, zdolnością do ruchu oraz bezwładnością. Właściwości te są według Newtona najbardziej podstawowymi cechami materii.

Reguła III pozwala nam też uogólnić liczne obserwacje i twier­dzić, że „wszelkie ciała obdarzone są zasadą wzajemnego ciążenia”. Ciężar nie należy wszakże do istoty ciał, mimo że jest właściwością powszechną. Jedyną wrodzoną siłą ciał jest niezmienna vis insita – siła bezwładności, ciężar danego ciała zależy natomiast od po­łożenia innych ciał, np. od jego odległości od Ziemi, może się więc zmieniać.

Reguła IV nie dozwala, aby hipotezy tworzone ad hoc mogły podważać wnioski oparte na indukcji wyprowadzonej z doświad­czenia. Dotyczy to, jak można się domyślać, hipotez tak łatwo wy­my­ślanych przez filozofów mechanistycznych.

Reguły sformułowane przez Newtona nie są tak oczywiste, jak sądził on sam, przeciwnie – widziane z perspektywy czasu uka­zują, jak trudno skodyfikować metody postępowania w naukach empirycznych. Ogromny naukowy autorytet Newtona sprawił jednak, że uznawano go często również za autorytet metodo­logiczny, naśladując bez zastrzeżeń ideał nauki deklarowany w Principiach. 

Aby wyprowadzić prawo powszechnego ciążenia, Newton od­wo­łał się do bezspornych jego zdaniem faktów obserwacyjnych: ruch satelitów Jowisza i Saturna, ruch planet wokół Słońca i ruch Księżyca wokół Ziemi podlegają prawu pól oraz III prawu Keplera.

Do tych faktów obserwacyjnych Newton zastosował następnie twier­dzenia udowodnione w I księdze Principiów. Udowodnił tam, że ruch, w którym spełnione jest prawo pól, zachodzi pod wpły­wem siły skierowanej do środka oraz że z III prawa Keplera wynika prawo odwrotnych kwadratów dla siły. Zatem satelity wokół planet i planety wokół Słońca poruszają się pod wpływem pewnej siły skierowanej do centrum i odwrotnie proporcjonalnej do kwadratu odległości.

Z kolei chciał wykazać, że siła utrzymująca Księżyc na orbicie jest tożsama z siłą ciężkości. Biorąc na promień orbity Księżyca 60 promieni Ziemi i korzystając ze zmierzonego przez Picarda w latach 1669-1670 promienia Ziemi (123 249 600 stóp paryskich) oraz znając okres obrotu Księżyca wokół Ziemi (27 dni 7 godzin 43 minuty) obliczył, że w ciągu minuty Księżyc spada o 15 ¹/₁₂ stóp paryskich. Zgodnie z prawem odwrotnych kwadratów, gdyby Księżyc znalazł się przy powierzchni Ziemi (tzn. 60 razy bliżej), przebywałby w ciągu minuty odległość 60²  razy większą, a więc równą 60 ´ 60 ´ 15 ¹/₁₂ stóp paryskich. W ciągu jednej sekundy przeby­wał­by zaś 15 ¹/₁₂ stóp paryskich (droga przebyta w jednostajnie przy­spieszonym spadaniu jest proporcjonalna do kwadratu czasu). Porównując tę liczbę z odległością przebywaną w ciągu sekundy przez ciała spadające na Ziemię, równą 15 stóp 1 ⁴ /₂₇ cala, wy­wnioskował, że siła, która utrzymuje Księżyc na orbicie, byłaby równa sile ciężkości, gdyby Księżyc znalazł się blisko Ziemi.

Według reguł I i II należało więc uznać, że to właśnie siła cięż­kości utrzymuje Księżyc na orbicie. Gdyby była to jakaś inna siła, to ciała spadałyby na Ziemię pod łącznym wpływem tej siły oraz siły ciężkości i musiałyby w sekundzie przebywać drogę dwa razy dłuższą niż wyliczona wyżej.

W Scholium po tym twierdzeniu Newton opisał eksperyment myślowy ilustrujący tę sytuację. Załóżmy, że Ziemia ma wiele księ­życów w różnych odległościach, tak jak Jowisz czy Saturn. Ich ruch musiałby podlegać również prawom Keplera, a więc znowu ozna­czałoby to, że siła dośrodkowa utrzymująca je na orbicie maleje jak kwadrat odległości. Wyobraźmy sobie, że księżyc najbliższy Ziemi porusza się na wysokości najwyższych gór na Ziemi. Zgodnie z do­piero co wykonanym rachunkiem siła dośrodkowa działająca na ten księżyc byłaby równa sile ciężkości na szczycie góry. A więc gdyby zatrzymać jego ruch orbitalny, księżyc ów zacząłby spadać dok­ładnie tak, jak spadają ciała ze szczytu tej góry. Chcąc uważać, że siła działająca na księżyc jest czym innym niż siła ciężkości, musielibyśmy przy tym zakładać, że prawdziwa siła ciężkości na niego nie działa. Takie samo spadanie objaśnialibyśmy inaczej w wypadku ciał spadających z góry (jako ciężkość), a inaczej w wypadku tego hipotetycznego księżyca, co przeczy dwóm pier­wszym regułom rozumowania.

Reguła II wymaga, abyśmy uznali, że również siły działające na satelity planet oraz siły działające na same planety, a skierowane ku Słońcu, są siłami ciężkości – inaczej prawa fizyki w okolicy Ziemi by­łyby inne niż, powiedzmy, w okolicy Jowisza. Wynika stąd, że wszy­stkie planety są ciałami ciężkimi, bo poruszają się same bądź są środkiem ruchu, a ponieważ każde oddziaływanie musi być na mo­cy III prawa ruchu wzajemne, przeto na każdą planetę działa cią­żenie, co więcej, ciążenie w kierunku danej planety musi maleć jak kwa­drat odległości. Wszystkie planety ciążą więc wzajemnie ku so­bie – dopóki doświadczenie nie każe nam przyjąć, że jest ina­czej, na­leży ciążenie uważać za powszechne, zgodnie z IV regułą.

Identyfikując siłę, która utrzymuje planety na orbitach, ze znaną wszystkim siłą ciężkości działającą na ciała przy powierzchni Ziemi, dokonał Newton najważniejszego kroku w ujednoliceniu obrazu świa­ta. Tym razem jednolitość materii i rządzących nią praw nie była już tylko filozoficznym postulatem, ale miała konsekwencje mo­ż­liwe do obliczenia i zmierzenia w obserwacjach. Pomysł grawi­ta­cji sięgającej Księżyca przyszedł mu do głowy dwadzieścia lat wcześniej, dopiero teraz jednak stał się fragmentem rozbudowanej i prze­myślanej ilościowej teorii. W latach sześćdziesiątych niezna­jomość dokładnej wartości promienia Ziemi spowodowała, że ten sam rachunek (ujęty wtedy jako porównanie ciążenia z siłą odśrod­kową) nie dał ścisłej zgodności liczbowej. Rozbieżność przypisał wtedy Newton działaniu wiru ziemskiego, w którym porusza się Księżyc. W okresie pisania Principiów niepotrzebna była żadna do­datkowa hipoteza.

Wszystkie ciała spadają na Ziemię jednakowo, jeśli tylko abstra­hować od oporu powietrza. Fakt ten Newton sprawdzał doświad­czalnie przez porównywanie ruchu wahadła o niezmiennej formie zewnętrznej (aby opór powietrza był stały), lecz wypełnionego materiałami tak rozmaitymi, jak złoto, srebro, ołów, szkło, piasek, sól, drewno, woda i zboże. Jak pisze, w doświadczeniach tych z łatwością wykryłby różnicę jednej tysięcznej części ilości materii odpowiadającej temu samemu ciężarowi. „Nie ma więc wątpliwości, że natura ciążenia jest ta sama na planetach i na Ziemi” – niezależnie od tego, z czego zbudowane są planety, ciążenie działa proporcjonalnie do ilości materii, tzn. do masy. Szybkość spadania na Słońce zależy więc tylko od odległości: tak samo spadają w kierunku Słońca np. Jowisz oraz jego satelity – wspólnie bowiem poruszają się wokół Słońca. Ewentualne różnice w ich ciężkości byłyby łatwe do zaobserwowania – zatem planety ze swymi księżycami są również czymś w rodzaju wahadła wykazującego, że ruch pod wpływem ciążenia nie zależy od rodzaju poruszającej się materii.

Ciężar nie zależy od kształtu i rozmieszczenia cząstek ciała, za­le­ży jedynie od masy. Wszystkie znane ciała mają ciężar, toteż należy uznać,  że nie ma ciał pozbawionych ciężaru. Oznacza to, że nie­ważki eter Kartezjusza nie istnieje.

Proporcjonalność ciężaru i masy oznacza, że siła ciążenia jest innego rodzaju niż siła magnetyczna – modelowy przykład przy­ciąga­­nia na odległość. Siła magnetyczna nie jest proporcjonalna do iloś­­ci materii. Niektóre ciała przyciągane są mocniej, niektóre słabiej, a niektóre w ogóle nie są przyciągane przez magnes. Ponadto si­­­ła magnetyczna, jak wynikało z eksperymentów New­tona, jest w przy­­­bliżeniu odwrotnie proporcjonalna do trzeciej potęgi od­ległości.

Doświadczenia dotyczące związku masy z ciężarem były w póź­niejszych wiekach wielokrotnie powtarzane, zawsze z takim samym wynikiem. Fakt, że wszystkie ciała poruszają się jednakowo pod wpły­wem ciążenia, pozostawał zadziwiającą właściwością sił gra­witacji, dopóki nie stał się, już w XX w., punktem wyjścia doskonalszej teorii ciążenia – ogólnej teorii względności Alberta Einsteina.

Newton nigdy nie sformułował jednego prawa powszechnego ciążenia, m.in. dlatego, że nie używał języka algebry. Podał jednak wszystkie właściwości ciążenia: jego powszechność, proporcjo­nalność do rozpatrywanych mas oraz zależność od odległości.

Teoria Newtona nie tylko objaśniała w jednolity sposób znane już prawa ruchu planet, lecz przewidywała również pewne zjawiska wywołane wzajemnym ciążeniem planet. Również komety poruszać się miały pod wpływem tego samego, powszechnego ciążenia ku pozostałym ciałom niebieskim. Zjawisko przypływów i odpływów morza można było objaśnić wpływem ciążenia wód ku Księżycowi. Grawitacja okazała się też siłą odpowiedzialną za kulisty kształt planet i Ziemi, co więcej, prawa mechaniki przewidywały lekkie spła­sz­czenie planet przy biegunach. Badaniu tych konsekwencji prawa powszechnego ciążenia Newton poświęcił większą część III księgi Principiów.

 

 

* * *

 

 

Już porównanie ciążenia na powierzchni Ziemi i w pobliżu Księ­życa kryje pewną subtelność. Obliczając ciężar ciała na Ziemi, np. jabłka, sumujemy siły ciążenia jabłka ku poszczególnym częściom Ziemi (które znajdują się przecież w najrozmaitszych odległościach od jabłka). Nie jest więc wcale oczywiste, że całkowity ciężar jabłka jest odwrotnie proporcjonalny do kwadratu odległości od środka Ziemi – a takie założenie przyjęte było w rozumowaniu. Newton udowodnił jednak w księdze I twierdzenie, że postępowanie to jest uprawnione, pod warunkiem że Ziemia ma kształt kulisty.

Prawo powszechnego ciążenia pozwoliło Newtonowi wysnuć wiele wniosków. Odwracając rozumowanie dotyczące Ziemi i jej Księ­życa mógł  na podstawie znanego ruchu księżyca planety obli­czyć ciążenie na jej powierzchni. To z kolei umożliwiało porówna­nie gęstości i mas planet. Po raz pierwszy można było też porównać masy planet (posiadających satelity) między sobą oraz z masą Słońca. Okazało się, że nawet masa największej z planet, Jowisza, jest 1067 razy mniejsza niż masa Słońca.

Obliczenia mas planet wywarły na współczesnych ogromne wra­żenie. Oto śmiertelnik uzykał dostęp do tajemnic stworzenia znanych jedynie Bogu. Na nagrobku Newtona przedstawiono gromad­kę putti z akcesoriami różnych prac wielkiego uczonego: z pryzma­tem, teleskopem, piecem. Jeden z chłopców zajęty jest ważeniem planet.

Na podstawie porównania gęstości Jowisza i Ziemi można było wywnioskować, że Jowisz ma mniej więcej gęstość lodu. Z doś­wiad­czeń II księgi wynikało, że kula z lodu poruszając się w powie­trzu traci 1/4586 swego ruchu na drodze równej swemu promie­niowi. Gdyby więc Jowisz poruszał się w takim ośrodku, jak po­wietrze, musiałby w ciągu 30 dni (w ciągu których przebywa 459 swoich promieni) tracić dziesiątą część swego ruchu, czego się oczywiście nie obserwuje. Oznacza to, że hipotetyczny ośrodek wy­peł­niający świat musiałby być niezmiernie rzadki w porównaniu z powietrzem. Raz jeszcze eter okazał się niemożliwy do wykrycia.

Ciążenie działa również na Słońce, zatem i Słońce nie może być nieruchome. Newton z wyraźną satysfakcją poprawił poprzedników: ani Ziemia, ani Słońce nie są absolutnie nieruchome. Nieruchomy jest środek masy całego układu planetarnego. Ponieważ masa Słoń­ca znacznie przewyższa masy planet, więc ruch wokół środka masy w praktyce oznacza krążenie wokół Słońca. Wielka masa Słońca sprawia też, że największe siły ciążenia działają między planetami a Słońcem, wzajemne zaś ciążenie planet ku sobie na ogół można pominąć.

Wyjątkem jest ciążenie Saturna ku największej planecie, Jowi­szowi. W chwilach największego zbliżenia obu planet siła ciążenia Saturna w kierunku Jowisza jest tylko 211 razy mniejsza niż jego ciążenie ku Słońcu. Również ruch Ziemi jest zauważalnie zaburzany przez Księżyc, tak że wokół Słońca porusza się nie środek Ziemi, lecz wspólny środek masy układu Ziemia-Księżyc.

Planety wirują wokół swoich osi, co sprawia, że ich materia poddana jest siłom odśrodkowym. Gdyby materia ta była ciekła, planety musiałyby przyjąć kształt spłaszczony przy biegunach. Wyraźne spłaszczenie obserwuje się u Jowisza, który szybko wiruje i jest dużo większy od Ziemi. Ziemia również powinna być spła­sz­czo­na, inaczej jej ruch wirowy musiałby spowodować wezbranie mórz w okolicach równika i zalanie lądów – jak spekulował Newton.

Rozważając równowagę wody w dwóch kanałach wydrążonych ze środka Ziemi do bieguna i równika, Newton doszedł do wnio­sku, że stosunek osi ziemskich wynosi 229:230. Podobne obliczenie dla Jowisza dało stosunek długości osi 10 1/3 : 9 1/3, co bliskie jest wynikom obserwacji.

Możliwość spłaszczenia Ziemi przyciągnęła uwagę uczonych. Kilka lat po ukazaniu się I wydania Principiów Christiaan Huygens na podstawie własnej teorii grawitacji obliczył, że spłaszczenie Zie­mi powinno być równe 577:578. Zmierzenie spłaszczenia Ziemi mogłoby zatem rozstrzygnąć o uznaniu którejś z dwóch teorii. Po­miary publikowane za życia Newtona wskazywały jednak raczej na to, że Ziemia jest wydłużona wzdłuż osi.

Najtrudniejszym zjawiskiem analizowanym w Principiach był ruch Księżyca – zawsze jeden z najbardziej kłopotliwych proble­mów astronomii matematycznej. Księżyc jest na tyle blisko Ziemi, że łatwo zaobserwować rozmaite drobne nieregularności jego ruchu. Prawa Keplera nie są w tym wypadku wystarczająco dokładne. Astronomowie opisują ruch Księżyca jako ruch po elipsie, która jednak ciągle zmienia położenie w przestrzeni (ryc. 24). Kąt nachylenia płaszczyzny orbity Księżyca do płaszczyzny orbity Ziemi zmienia się okresowo. Linia przecięcia obu płaszczyzn – tzw. linia węzłów – obraca się w płaszczyźnie orbity Ziemi, w kierunku prze­ciwnym do Księżyca, wykonując pełny obrót w ciągu ok. 19 lat. Ponadto w samej płaszczyźnie orbity Księżyca oś wielka elipsy, czyli linia łącząca perigeum i apogeum – tzw. linia apsyd – obraca się w kierunku ruchu Księżyca w okresie niecałych 9 lat. Również kształt orbity, mierzony wielkością jej mimośródu, zmienia się okresowo. Główną przyczyną tych wszystkich odstępstw od ruchu po idealnej elipsie stanowi, jak odkrył Newton, silne ciążenie ku Słońcu, nakładające się na ciążenie ku Ziemi. Ruch Księżyca sta­nowi zatem przykład zagadnienia trzech ciał.

Zainteresowanie ruchem Księżyca miało aspekt praktyczny. Żegluga oceaniczna potrzebowała prostych sposobów wyznaczania położenia geograficznego okrętu. Szerokość geograficzną wyznacza się łatwo na podstawie obserwacji Słońca lub gwiazd, ale dla wyz­na­czenia długości należy porównać czas miejscowy z jakimś stan­dar­dowym czasem, np. na południku Greenwich lub Paryża. Ówczesne zegary źle znosiły podróże, dlatego próbowano wyko­rzystać zjawiska astronomiczne jako swoisty kosmiczny zegar. Szczególnie dobrze nadaje się do tego celu Księżyc, ponieważ poru­sza się wśród gwiazd mniej więcej o średnicę swojej tarczy w ciągu godziny. Należałoby tylko ułożyć wystarczająco dokładne tablice jego ruchu.

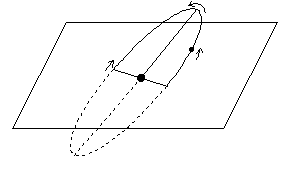Ryc. 24 Położenie orbity Księżyca względem płaszczyzny orbity Ziemi

Teoria grawitacji dała możliwość obliczenia ruchu Księżyca jako rezultatu ciążenia ku Ziemi i dalekiemu, lecz masywnemu Słońcu. W księdze I Newton analizował jakościowo, co powinno się dziać z orbitą tak zakłócanego ciała. Pokazał, że linia węzłów powinna się cofać, linia apsyd zaś poruszać w tym samym kierunku co ciało. Przewidywał też okresowe zmiany nachylenia orbity i odstępstwa od keplerowskiego prawa pól (zaburzająca siła nie jest już skie­rowana ku centrum Ziemi, bo pochodzi od Słońca). W księdze III obliczył wielkości liczbowe wielu z tych efektów. Zgodność z ob­serwacjami była na ogół dobra, np. szybkość cofania się węzłów orbity otrzymał z dokładnością 1/400. Przy okazji wyjaśnił, jak zaburzenia zależą od odległości Słońca od Ziemi, co przejawia się w rocznych zmianach pewnych parametrów.

Teoria Księżyca, aczkolwiek poprawiona później w drugim wydaniu Principiów, była jednak wciąż niezadowalająca. Newton mówił, że głowa go boli, gdy myśli o ruchu Księżyca. Powtarzał, że ma wciąż za mało obserwacji. Pisał do Flamsteeda próbując go prze­konać, aby tamten przekazał mu swoje obserwacje Księżyca, które kiedyś zostaną może należycie ocenione:

Ale kiedy to będzie, Bóg wie; obawiam się, że nie za pańskiego życia, jeślibym umarł, zanim to zostanie zrobione. Znajduję bowiem tę teorię tak bardzo zawiłą, a teorię grawitacji tak do niej niezbędną, iż jestem przekonany, że nie będzie udoskonalona jak tylko przez kogoś, kto rozumie teorię grawitacji równie dobrze albo lepiej niż ja [10, 40, 43].

Newton zapowiadał również, że mając obserwacje w ciągu kilku mie­sięcy zbuduje teorię Księżyca. Flamsteed, który nie dowierzał teo­re­tycznym spekulacjom i niezbyt rozumiał teorię grawitacji, wi­dział w tych wypowiedziach arogancję i chęć wykorzystania cudzej pracy. Zadanie było trudniejsze, niż sądzili obaj. Postęp w teorii Księ­życa wymagał doskonalszych narzędzi matematycznych i osią­gnię­ty został dopiero w drugiej połowie XVIII wieku w pracach Clairauta, d'Alemberta i przede wszystkim Eulera.

Największą porażką Newtona w teorii Księżyca było obliczenie ruchu linii apsyd. Jedno z najznakomitszych twierdzeń Principiów pozwalało obliczyć ruch linii apsyd dla sił o zadanej postaci. Obli­czony w ten sposób obrót linii apsyd wywołany działaniem Słońca równa się 1^o  31' 28'' na każdy obieg. Pedantyczna dokładność była tu jednak nie na miejscu: wielkość obserwowana jest dwa razy więk­sza. Newton nie komentował uzyskanego przez siebie wyniku, uważając zapewne, że twierdzenie może być przynajmniej punktem wyjścia do dalszej pracy na ten temat. Dopiero w III – ostatnim za życia autora – wydaniu Principiów, gdy już było wiadomo, że nie uda się poprawić wyniku, umieścił Newton za liczbową wartością suchy komentarz: „jest to w przybliżeniu połowa ruchu apsyd Księżyca”. Prawidłową wartość ruchu apsyd można byłoby otrzy­mać, zmieniając nieco wykładnik potęgi w prawie grawitacji: z 2 na 2 ⁴/₂₄₃ . Wszelako Newton (w przeciwieństwie do niektórych swoich następców) nigdy nie traktował poważnie możliwości, aby prawo ciążenia mogło mieć tak nieelegancką postać.

Teoria Newtona pozwalała też wyjaśnić zjawisko pływów jako wynik ciążenia w kierunku Księżyca oraz Słońca. Cząstki wody znaj­­­dujące się na powierzchni Ziemi ciążą ku Księżycowi słabiej lub mocniej, zależnie od ich odległości od Księżyca. Różnica tej siły i śre­d­niej siły, jaka działa na materię Ziemi ze strony Księżyca, jest właśnie siłą wywołującą pływy. Dla punktów Ziemi bliższych Księżyca przeważa siła ciążenia ku Księżycowi, więc wypadkowa siła jest skierowana w jego stronę. Dla punktów Ziemi dalszych od Księżyca siła ciążenia ku Księżycowi jest mniejsza niż wartość śred­nia, więc wypadkowa siła jest skierowana od Księżyca. W rezultacie po obu stronach Ziemi mamy do czynienia z siłami skierowanymi do góry, powodującymi przybieranie wód (ryc. 25). Gdyby cała po­wie­rz­chnia Ziemi pokryta była wodami, wody te przybrałyby kształt mniej więcej elipsoidy zwróconej dłuższą osią w kierunku Księżyca (a właściwie w kierunku, w którym kilka godzin wcześniej znaj­dował się Księżyc, ruch wody jest bowiem opóźniony w stosunku do wymuszającej go siły z powodu tarcia o dno, bezwładności itd.). W ten sposób został wyjaśniony półdobowy okres pływów oraz ich związek z Księżycem. Również Słońce powinno wywierać podobne, choć słabsze, działanie na wody mórz. Pod wpływem ciążenia ku Słońcu wody przybierają kształt elipsoidy zwróconej w jego kie­runku. Oba efekty przypływowe wzmacniają się bądź osłabiają, zależnie od usytuowania obu ciał niebieskich. Zjawisko to było zresztą obserwowane od dawna: przypływy są największe, gdy Księżyc jest w nowiu albo w pełni, czyli gdy znajduje się w jednej linii ze Słońcem.

Ryc. 25 Przypływy i odpływy mórz

Jeszcze jednym zjawiskiem wyjaśnionym przez Newtona jest pre­cesja punktów równonocy. Od starożytności było wiadomo, że bie­gun niebieski przesuwa się powoli wśrod gwiazd. Względem gwiazd to oś ziemska zmienia kierunek, zataczając stożek w okresie około 26 000 lat (ryc. 26). W teorii Newtona precesja okazała się skutkiem spłaszczenia Ziemi. Rozpatrzył on najpierw pierścień ma­te­rii o kształcie obwarzanka i promieniu równym promieniowi Ziemi, poruszający się wokół Słońca w ciągu roku i nachylony do płaszczyzny orbity tak jak równik Ziemi. Do pierścienia można zastosować twierdzenie o zaburzeniach ruchu orbitalnego przez ciążenie w kierunku trzeciego oddalonego ciała, to samo, które sta­ło się podstawą teorii Księżyca. Ten sam efekt, który dla Księżyca był cofaniem się węzłów, dla pierścienia będzie oznaczać precesję. Jeśli teraz spłaszczoną Ziemię potraktujemy jako kulę z dodatkiem pierścienia materii w okolicy równika, to wyniki powinny stosować się i do niej.

Ryc. 26 Precesja punktów równonocy

Newton oblicza wielkość precesji wywołanej wpływem Słońca i Księ­życa, otrzymując obserwowaną przez astronomów wartość. Podobnie jednak jak w wypadku prędkości dźwięku wartość ta jest wyni­kiem zręcznego dobrania danych liczbowych, stosunek siły przypły­wowej Księżyca i Słońca był bowiem przez Newtona dwu­krotnie zawyżony. Bezspornym sukcesem Newtona jest samo osza­co­wanie wielkości precesji i wykazanie, że zjawisko to jest nieu­chronną konsekwencją prawa ciążenia. W teorii Newtona kierunek precesji świadczył o tym, że Ziemia jest spłaszczona przy biegunach, nawet jeśli wyniki pomiarów kształtu Ziemi wyraźnie tego nie potwierdzały.

Najbardziej bezpośrednim zastosowaniem teorii grawitacji był jednak ruch komet wokół Słońca. Ruch ten nie jest bynajmniej nie­re­gularny, jak dowodził Kartezjusz. Komety jak wszystkie ciała nie­bie­skie poruszają się pod wpływem siły ciążenia w ośrodku nie stawiającym żadnego oporu. Ich ruch jest więc równie przewi­dywalny jak ruch planet. Komety muszą poruszać się po jednej z krzywych stożkowych: elipsie, paraboli lub hiperboli ze Słońcem w ognisku. Trudność polegała tu jednak na znalezieniu metody okre­ślania orbity na podstawie obserwacji z Ziemi. Obserwacje astrono­miczne dostarczają informacji jedynie o kierunku, w którym znaj­duje się kometa, i należy wykorzystać fakt, że nasze stanowisko obserwacyjne – Ziemia – porusza się pomiędzy kolejnymi obser­wacjami. Jeszcze w połowie 1686 roku Newton nie potrafił poradzić sobie z problemem wyznaczenia orbity i narzekał na czas stracony nad tym zagadnieniem. W końcu wszakże udało mu się znaleźć me­todę określania orbity z trzech obserwacji i obliczył za jej pomocą orbitę wielkiej komety lat 1680-1681, nie uważając jej już za dwie oddzielne komety. Zakładał przy tym, że orbita ma kształt paraboli. Z obliczeń wynikało, że komety przechodzą blisko Słońca, a nie przebywają na obrzeżach układu planetarnego, jak utrzymywał Kartezjusz. Matematyczny problem wyznaczania orbit ciał niebies­kich na podstawie obserwacji był rzeczywiście trudny i lepszą me­to­dę obliczeń podać miał dopiero w XIX w. Carl Friedrich Gauss.

Wiele szczegółowych wyników Principiów miało być z czasem poprawionych, wiele wniosków było przedwczesnych, zdarzały się również błędy. Sam Newton sądził o nich , że „jeśli nie są wynikiem złego rozumowania, nie mają wielkiego znaczenia i mogą być po­prawione przez czytelnika”.

Principia ukazują wręcz niewiarygodną na tle ówczesnej nauki sprawność matematyczną i wyobraźnię teoretyczną Newtona. Tam, gdzie było to możliwe, uzyskiwał dokładne rozwiązania, w  innych zaś przypadkach potrafił niemal zawsze znaleźć jakieś przybliżenie pozwalające na efektywne obliczenia. Nie ulega wątpliwości, że tak ogromnej pracy nie potrafiłby wykonać żaden ze współczesnych Newtonowi uczonych.